All published articles of this journal are available on ScienceDirect.
A Review on the Characteristics of the Smear Zone: Field Data Back Calculation Compared with Laboratory Testing
Abstract
Background:
The so-called smear zone is a disturbed zone developed in soil during prefabricated vertical drainage (PVD) installation using a mandrel. There are 2 main parameters typically used to characterize the smear zone. First, the extent ratio signifies the extent of the soil damage due to mandrel penetration; and second, the permeability ratio κ represents the degree of disturbance to the soil permeability within the smear zone.
Objectives:
This study reviews 2 methods employed by various researchers to obtain the values for the 2 aforementioned parameters, i.e. 1) field data back calculation and 2) laboratory testing. It is found that the s’ values vary between 2.0 – 5.0 and between 2.0 – 6.3 based on field data back calculation and laboratory testing, consecutively. On the other hand, the κ values vary between 2.0 - 13.8 and 1.03 – 3.13 based on field data back calculation and laboratory testing, consecutively.
Results and Conclusion:
With regard to the previous studies, three causes of the variation are suggested in this study: 1) the laboratory testing’s inability to model the complexity of field conditions, 2) the absence of standardized laboratory methods that can be used as references and 3) the level of disturbance in the field which is considerably greater than that in the laboratory and differs at each research location. In addition to the review, historical data of a trial embankment at the embankment of the multi-purpose container yard in Kuala Tanjung, North Sumatra, Indonesia, are exhibited to illustrate the estimation of the s’ and κ values.
1. INTRODUCTION
In the last two decades, the use of a prefabricated vertical drainage known as PVD has been recognized as a very effective and efficient soil improvement method in preloading sites composed of soft soil deposits [1, 2]. Smear zone is a disturbed zone in the ground developed during PVD installation using a mandrel. The insertion of the mandrel disturbs the soil around the PVD area to a certain extent and consequently reduces the permeability of the soil k in this area. The permeability reduction in turn inhibits significantly the horizontal consolidation of the soft soil, known as the smear effects which eventually degrade the effectiveness of the PVD [3, 4]. Due to their significant impact, many researchers have been interested in examining the smear zone characteristics [5-11].
There are two propositions to delineate the smear zone, i.e. the two-zone and the three-zone hypotheses as presented in Fig. (1). The two-zone hypothesis, described among others by Bergado et al., (1991) [6] and Chai and Miura (1999) [12], divides the ground around the PVD into the smear zone and the undisturbed zone. The three-zone hypothesis, proposed among others by Sharma and Xiao (2000) [3], divides the ground around the PVD into 3 zones, i.e. the smear zone, the transition zone, and the undisturbed zone.
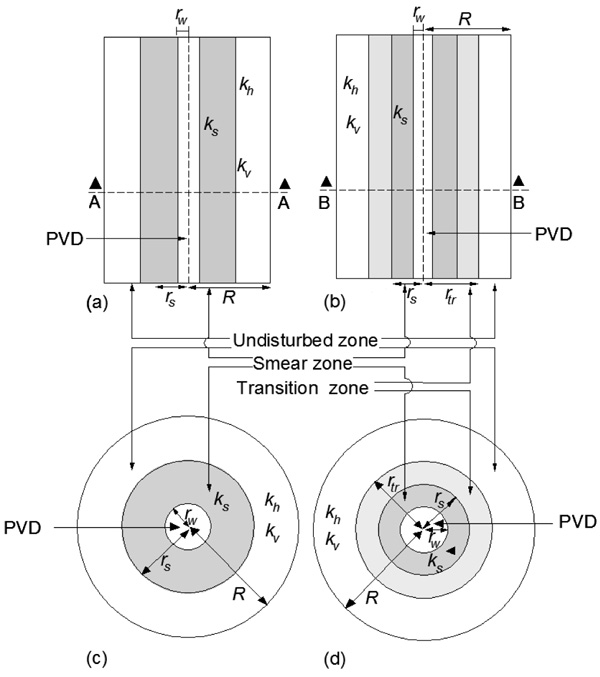
The main parameters proposed for characterizing the smear zone are the extent ratio and the permeability ratio. The extent ratio s or s’ is the ratio of the radius of the smear zone rs to the radius of the drain rw or the radius of mandrel rm, respectively. Hence s = rs/rw or s’ = rs/rm represents the range of disturbance due to the penetration of the mandrel on the treated ground. The permeability ratio κ is the ratio of the horizontal permeability kh at the undisturbed location to that at the disturbed site ks. Hence κ = kh/ks represents the degree of disturbance due to penetration of the mandrel on the soil permeability. These ratios become the 2 key values in PVD planning which will in turn affect the rate and duration of consolidation. The values can be estimated using analytical technique, field data back calculation (or numerical method), laboratory testing, or field testing.
A comprehensive standard method for determining them has not yet been established. Field data back calculation (or numerical method) and laboratory testing are among the more frequent applied methods. Researchers who characterized the smear zone with back-calculation of field data did simple curve fitting in their analysis [6-10]. Several other researches exercised field data back calculation coupled with finite element analysis [11-19], however, field investigation combined with laboratory test could also be conducted for the same purpose [20]. Alternatively investigators performed laboratory testing to obtain the characteristic values [3, 6, 9, 21-34]. Those whose results are compared in this study can be seen in column 2 in Tables 1 and 2, for field data and laboratory testings consecutively.
Due to the limitation of the soil lab model, the s’ and κ values resulting from laboratory testing results can not be directly used for planning without proper insights. This study aims to document and evaluate what components in the field that are extremely difficult to model in the laboratory and what disturbances may occur on the ground when the PVD works. This study includes historical data of a trial embankment for an illustrative purpose. It is hoped that the review made in this study will illuminate the subject on the smear zone especially in terms of field data and laboratory testing so that further research and advances in PVD technology may be assisted.
2. BASIC THEORY
2.1. Analytical Solution
The settlement for one-dimensional consolidation Sp can be given by Eq. (1)
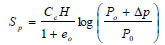 |
(1) |
where Cc = compression index, H = layer thickness, e0 = initial void ratio, Po = effective vertical stress and Δp = additional effective vertical stress. Assuming equal strain and pure radial flowing, the average degree of consolidation on cell units 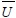 , including the smear effect and excluding the well resistance effect, can be expressed analytically as follows [35], (Eq. 2):
, including the smear effect and excluding the well resistance effect, can be expressed analytically as follows [35], (Eq. 2):
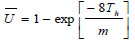 |
(2) |
where Th = the time factor in the horizontal direction and m = the s and κ dependent parameters, both of which are expressed as Eq. (3 and 4):
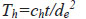 |
(3) |
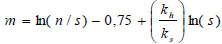 |
(4) |
where n = re/rw and ch = the horizontal consolidation coefficient, and t = the time in days.
Note that [35] assumed a constant smear effect resulting in constant reduced permeability in the smear zone. Walker and Indraratna (2006) [36] suggested a parabolic distributed smear effect in the smear zone, and they subsequently proposed the expression for m as Eq. (5):
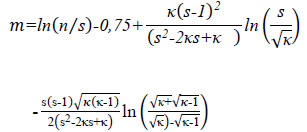 |
(5) |
In contrast Rujikiatkamjorn and Indraratna (2009) [37] assumed a linearly distributed smear effect on the smear zone and offered the expression for m as Eq. (6):
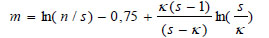 |
(6) |
2.2. Coefficient of Permeability
The coefficient of permeability of the soil layer measured in situ using field apparatus is typically greater than that measured in the laboratory using for example oedometer. In this regard, Tavenas et al., (1986) [38] stated the relationship of the permeability coefficients (Eq. 7):
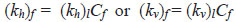 |
(7) |
where kh and kv are the horizontal and vertical permeability coefficients, consecutively, subcripts f and l denote values determined in the field and in the laboratory, consecutively, and Cf is the ratio of the permeability coefficient from the field to that from the laboratory. The ratio Cf depends on the sensitivity of the soil, macropore, and stratification of the soil layer.
As indicated by several researchers, laboratory testing may be the correct way to determine the magnitude of the coefficient of permeability in the smear zone ks Chai and Miura (1999) [12]. However it should be noted that because of the disruption in the sample and the comparatively small sample sizes, the laboratory permeability coefficient kl is less than field permeability coefficient value kf. Chai and Miura (1999) [12] admitted many uncertainties that exist in determining the kh/ks ratio in the field and proposed:
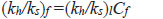 |
(8) |
For the planning and the implementation of PVD, the value for Cf in Eq.(8) should take into account the disturbance components that affect the permeability in the ground during the PVD work in the field.
2.3. Geotechnical Instruments
In order to observe the underground conditions during ground treatment, several geotechnical instruments are installed to measure realistic conditions beneath the soil surface. The commonly installed instruments are pneumatic piezometer for measuring excess pore water pressure, water standpipes for measuring water level, settlement plate for observing surface settlement, extensometer for gauging settlement at certain depths, and inclinometer for perceiving horizontal deformation.
3. IMPORTANT NOTES OF THE FIELD WORKS
The field work starts usually from land clearing and stripping. These are followed by spreading the geotextile separator layer and the sand blanket layer on top of the separator layer, and then the sand blanket can be compacted. Subsequently, installation of geotechnical instruments, including pneumatometer piezometer, water standpipe, settlement plate, and inclinometer, is made. Lastly, PVD installation and preloading can be conducted.
The factors that may cause different disturbances to the soil during the PVD work include depth of installation, thickness of sand mat, patterns of installation, PVD interval, mandrel shape and dimension, height of embankment, and speed of installation. These factors vary between locations which are indicated in columns 3 up to 10 in Table 1, and their influences on the smear zone characteristics are discussed later in this paper.
| No. | Researchers | Depth of Installation (m) | Sand Mat Thickness (mm) | Patterns Installation |
Installation Distance (m) |
Mandrel | Height of Embankment (m) |
Speed of Installation (mm/s) |
Type of Soil |
Field Data Back-Calculation |
s’=rs/rm or s= rs/rw* |
κ= kh/ks | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shape |
Dimension (mm2) |
||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | Bergado et al. (1991) [6] | 8.0 | 1,000 | Square | 1.2 | Rectangular | 45 x150, 150 x150 |
Soft Clay, Bangkok | Analytical | 2.0 | kh= kv | ||
| 2 | Bergado et al. (1992) [7] | 8.0 | 300 | Triangle | 1.5 | Rectangular | 150 x 45 | 4.00 | - | Soft Clay, Bangkok | Analytical | 2.5 * | 10.0 |
| 3 | Bergado et al. (2000) [8] | 12.0 | 1,500 | Square | 1.0; 1.2; 1.5 | Rectangular | - | 4.20 | - | Soft Clay, Bangkok | Analytical | 2.0 | 5.0 |
| 4 | Saowapakpiboonet et al. (2010) [9] | 10.0 | - | Triangle | 0.85 | Rectangular | - | - | - | Soft Clay, Bangkok Soft Clay, Bangkok | Analytical Analytical |
2.0 2.0 |
7.2 6.6 (+v) |
| 5 | Hiep and Chung (2018) [10] |
30.0 – 35.0 | 500 - 800 | Triangle | 1.5 | Rectangular | 120 x 80 | 6.00 - 8.00 | - | Clay, Mekong Delta | Analytical | 2.0 | 2.0 |
| 6 | Indraratna and Redana (2000) [11] | 12.0 18.0 |
1,500 - |
Square Triangle |
1; 1.2; 1.5 1.3 |
Rectangular Rectangular |
- - |
4.20 - |
- - |
Soft Clay, Bangkok Muar Clay Deposit | FEM FEM |
4-5 * 4-5 * |
kh = kv kh = kv |
| 7 | Chai and Miura (1999) [12] |
25.0 | 500 | Square | 1.5 | Rectangular | - | 3.50 | - | Soft Clay, Ariake | FEM | 3.0 | 10.0 |
| 8 | Chai et al. (1995) [13] | 18.0 | - | Triangle | 1.2 | Rectangular | - | 4.70 | - | Muar Clay Deposit | FEM | 4.2 * | 2.0 |
| 9 | Chai et al. (1996) [14] | 18.0 12.0 |
- - |
Triangle Square |
1.2 1.5 |
Rectangular Rectangular |
- 120 x 60 |
4.70 - |
- - |
Muar Clay Deposit Soft Clay, Bangkok |
FEM FEM |
3.0 3.0 |
10.0 10.0 |
| 10 | Chai et al. (2001) [15] | 19.0 | 500 | Triangle | 1.5 | Rectangular | - | - | - | Mucky Clay | FEM | 6.7 * | 13.8 |
| 11 | Indraratna et al. (2008) [16] |
12.0 | - | Triangle | 1.5 | Rectangular | - | 1.50 | - | Soft Clay, Swedish | FEM | 2.0 * | 4.0 |
| 12 | Pajouh et al. (2013) [17] | 9.0 | - | Square | 1.0 | Rectangular | - | 3.00 | - | Soft Clay, Chittagong | FEM | 3.0 | 2.0 |
| 13 | Pajouh et al.(2014) [18] | 11.0 9.0 |
650 - |
Triangle Square |
2.0 1.0 |
Rectangular Rectangular |
- - |
2.85 3.00 |
- - |
Silty Clay Soft Clay, Chittagong |
FEM FEM |
3.0 3.0 |
4.0 2.0 |
| 14 | Pajouh et al.(2014) [19] | 24.0 22.0 11.00 |
1,500 650 650 |
Square Triangle Triangle |
1.0 1.35 2.0 |
Rectangular Rectangular Rectangular |
- - - |
8.50 5.00 2.80 |
- - - |
Soft Clay, Ballina Soft Soil Silty Clay |
FEM FEM FEM |
4.0 5.0 3.0 |
4.0 5.0 4.0 |
| 15 | Bo et al. (2003) [20] | 50.0 | Square | 2.2, 5.3 | Rectangular Rhombus |
120 x 60, 145 x 90 |
300 - 600 300 - 600 |
Marine Clay, Singapore | Field and Laboratory Test | 4.0-7.0 | 2.0-10.0 | ||
| 16 | The Case study | 17.0 | 600 | Triangle | 1.5 | Rectangular | 120 x 50 | 5.20 | 400 - 500 | Soft Soil, North Sumatra | Analytical | 3.0 | 7.0 |
As previously mentioned, the characteristics of the smear zone are normally estimated by the back calculation method using the data resulting from the geotechnical instrument. The estimation is conducted based on the obtained time dependent settlement data which are then fitted with Eq. 1 or processed with a numerical program. However, Bo et al., (2001) [39] did field testing to determine the values of s’ and κ using field apparatus. Table 1 summarizes 16 data set on soil improvement conditions from various locations using PVD. Note in the table that the extent ratio and the permeability ratio are given in the last two columns.
4. IMPORTANT NOTES OF LABORATORY WORKS
Tests in the lab are conducted without referential standards. Nevertheless, the shapes of laboratory soil tanks used are typically cylinders and boxes. Previous researchers had different h/d ratios from one and another as shown in column 3 in Table 2. Note that h and d are the height and the diameter of the cylindrical soil tank, consecutively. In contrast, Tran-Nguyen and Edil (2011) [26] developed the box-shape tank which then further utilized by Sengul, et al. (2016) [33]. Before placed in the soil tank, the sample is tested for the basic soil properties including moisture content w, liquid limit LL, plastic limit PL, void ratio e, spesific gravity Gs, unit weight soil γ, compression index cc, and swelling index cs.
| No. |
Researchers |
Tank Dimension |
Basic Soil Properties |
Sample Preparation |
Stress | PVD Dimension (mm2) |
Mandrel (mm2) |
Speed of Installation ( mm/s) |
Extent Ratio | Permeability Ratio κ = kh/ks |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (kPa) | ||||||||||||||||||||
|
s’=rs/rm or s = rs/rw* |
||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||||||||||
| 1 |
Sharma and Xiao (2000) [3] 3 zones |
h=400 mm d=1000 mm h/d=0.40 | Reconstituted Kaolinite w=65%, LL=70%, PL=40%, e =1.4, Gs=2.61 |
Kaolinite is mixed water up to w = 2 x LL, put into consolidation tank and be vacuumed for stress at 90 kPa for several days. |
Po = 100 ΔP = 1,102 |
SD diam.= 50 mm |
Circular diam. =50 mm |
5.0 | 4.0 * |
1.3 |
||||||||||
| 2 | Bergado et al. (1991) [6] 2 zones |
h=920 mm d=455 mm h/d=2.02 |
Reconstituted Soft Bangkok Clay γ=14.7 kN/m3, Cc=0.80, Cs=0.13, e = 2.3 |
Samples are placed in cell consolidation layer by layer. Sand of 5 cm thick is given on the surface. |
Po = 10.2 ΔP = 47.8 |
40 x 6 | 60x60 Recta- ngular |
- | 2.0 | 1.5 – 2.0 | ||||||||||
| 3 |
Saowapakpiboon et al. (2010) [9] 2 zones |
h=500 mm d=305 mm h/d=1.64 |
Reconstituted Soft Bangkok Clay w=113%, LL= 102%,PL=40%, Gs=2.66, γ =14.7 kN/m3 |
The sample is taken into 3-4 m from the ground surface and placed in the cell consolidometer coating. |
- ΔP = 100 |
100 x 3.5 |
- |
- |
2.0 2.0 (+v) |
2.7 2.5 |
||||||||||
| 4 | Indraratna and Redana (1998) [21] 2 zones |
h=950 mm d=450 mm h/d=2.11 | Reconstituted Alluvial Clay, Sydnay w =40%, LL=70%, PL=30%, Gs=2.6, γ =17.0 kN/m | Samples are mixed with water, placed in a consolidometer cell and compacted layer by layer. Surface is given sand 5 cm. |
Po = 20 ΔP = 200 |
SD diam.= 46 mm | Circular diam. = 50 mm |
- | 4.0 - 5.0 | kh/kv = 1.15 | ||||||||||
| 5 | Indraratna and Rujikiatkamjorn (2004) [22]. 2 zones |
h=950 mm d=450 mm h/d=2.11 |
Reconstituted Alluvial Clay, Moruya w = 45%,LL= 42%, PL=17%, Gs=2.6, γ =17.0 kN/m3 | Samples are mixed with water up to w slightly larger than LL, placed in a coating,compacted using consolidometer cell. |
Po=20 ΔP = 30+50 |
100 x 3 | 125 x 25 Recta- ngular |
- | 3.0 * 3.0 * (+v) |
kh/kv= 1.17 - 1.20 |
||||||||||
| 6 | Sathananthan and Indraratna (2006) [23] 2 zones |
h=1040 mm d=650 mm h/d=1.60 | Reconstituted Alluvial Clay, Moruya w=45%, LL= 42 %, PL=17%, Gs=2.6, γ =17.0 kN/m3 | Clay is mixed with water, kept on container for several days, placed in coating consolidometer cell (150 mm/Layer), and compacted. |
Po = 20 ΔP = 200 |
100 x 3 | 125 x 25 Recta- ngular | 8.3 | 2.5 | 1.34 | ||||||||||
| 7 | Feng and Yin (2006) [24] 2 zones |
h=450 mm d=300 mm h/d=1.50 | Reconstituted Hongkong Marine Clay, w = 85,6 %, LL= 51.1 %, PL=26.1 %, Gs=2.58 | Clay is mixed with water and stored in container for several days, placed in coating consolidometer cells (150 mm/ layer) and compacted. |
Po = 20 ΔP = 80 |
50 x 5 | 60 x 13 Recta- ngular | - | 2.0 | 2.0 | ||||||||||
| 8 | Shin et al. (2009) [25] 2 zones |
h=1000 mm d=700 mm h/d=1.43 | Reconstituted Busan Clay w=56 %, LL= 46.4 % PL= 24.1 %, Gs= 2.64 |
The test sample passed the sieve No.40. is mixed with water up to w = 2 x LL. The trapped air is removed by vacuum during mixing. |
Po = 50 ΔP = 200 |
85 x 6.4 | 100 x 50 Recta- ngular |
20.0 | 4.0-4.2 (l) 3.3-3.4 (s) |
- - |
||||||||||
| 9 | Tran-Nguyen and Edil (2011) [26] 2 zones |
h=530 mm we= 350 mm t = 130 mm |
Reconstituted HRK, LL=49 %, PL=24 %, Gs=2.59 | Sample with w equal to the field is placed on the box, placed in SZM instrument coating, and compressed with vibrator. |
Po = 25 i = 20-30 |
100 x 3.2 | 15 x 120 Recta- ngular |
1.0-2.5 | 3.0 (HRK) | 1.03 |
||||||||||
| Reconstituted CID LL = 49 %, PL=20-25 %,Gs= 2.71 |
4.2 (CID) | 1.25 | ||||||||||||||||||
| 10 | Ghandeharioon et al. (2012) [27] 3 zones |
h = 900 mm d = 650 mm h/d=1.38 |
Reconstituted Lucustrine LL= 55 %, PL=27 %, e = 1.46 |
Sample is mixed with water until w = 1.1 x LL, placed in cell consolidometer layer by layer, and compacted. |
Po = 20 ΔP = 50 |
100 x 4 | - | - | 2.65 | kh/kv= 1.2 - 1.6 |
||||||||||
| 11 | Chai et al. et al.(2013) [28] 2 zones |
h =700 mm d = 450 mm h/d =1.56 |
Reconstituted Soft Bangkok Clay w=113%, LL=104%, PL = 45%, Gs = 2.66, γ =14.7 kN/m3 |
Samples are placed in cell consolido- meter layer by layer. |
Po = 50 ΔP = 100 |
50 x 3.5 | 81.9 x18.2 Recta- ngular |
- | 2.0 | 3.0 | ||||||||||
| 12 | Rujikiatkamjorn et al.(2014) [29] 3 zones |
h = 561 mm d = 345 mm h/d =1.60 |
Undisturb Bulli Clay w = 41%, LL= 50%, PL=25%, Gs=2.62, γ=18.5 kN/m3 |
The soil around the sample is dug and cut from base, wrapped to prevent loss of w, stored in a humidity- controlled room, and placed into cell consolidometer. |
Po = 20 ΔP = 200 |
we = 50 | 55 x 5 Recta- ngular |
- | 3.7 | 1.33 - 2.85 | ||||||||||
| 13 | Indraratna et al (2015) [30] 2 zones |
h =25,4 mm d= 63,5 mm h/d =0.40 |
Undisturb Ballina Clay w=94,7% ,LL=98%, PL=32%, Gs=2.58, e =2.44, γ=16.5 kN/m3 |
Samples for Oedometer testing are collected from around the PVD installed in the field. A series oedometer testing is performed. |
ΔP = 200 | 100 x 3 | 120 x 60 Recta- ngular |
- | 6.3 | 2.7 | ||||||||||
| 14 | Joseph et al. (2015) [31] 2 zones |
h = 600 mm d= 600 mm h/d=1.00 |
Reconstituted Cochin Marine Clay w = 112%, LL = 156%, PL = 34 %, Gs = 2.62 |
Sample is placed into the tank of consolidometer, with w = LL layer by layer. |
Po = 5 ΔP = 120 |
SD diam. = 46 mm |
Circular diam. = 50 mm |
hammer wi=2.6 kg hi=30 cm |
5.0 - 6.0 | 1.3 - 1.4 | ||||||||||
| 15 | Pajouh et al. (2015) [32] 2 zones |
h =200 mm d = 250 mm h/d =0,80 |
Reconstituted Kaolinite, bentonite w =120%, LL = 67-87%, PL=27-34%, PI=40-43% |
Samples are mixed with water to w= (1.4 -1.8) LL, placed into Rowe cell, given stress cell =110 kPa,and back pressure =100 kPa for saturation. |
Po = 20 ΔP = 200 |
SD diam. = 22 mm |
Circular diam. = 25 mm | - | 3.0 * | 4.0 | ||||||||||
| 16 | Sengul et al. (2016) [33] 2 zones |
h =530 mm we= 350 mm t = 130 mm |
Reconstituted HRK,LL=51%, PL=26%, IP=25%, Gs=2.60 |
Samples with w equal to the field are placed on the box, placed in SZM instrument coating, and compressed with vibrator. |
Po = 25 Δh = 50 |
130 x 18 | 120 x 15 Recta- ngular |
2-5 |
3.3 | 2.0 | ||||||||||
| Reconstituted CID, LL=51%, PL=30%, IP=21%, Gs=2.76 |
2.3 - 2.4 | 2.86 - 3.13 | ||||||||||||||||||
| 17 | Choudhary et al. (2016) [34] 2 zones |
h =450 mm d = 650 mm h/d = 0.69 |
Reconstituted Balina Clay w = 94%, LL= 98%, PL=32%, Gs=2.6 |
Clay is taken 2 m below ground surface, mixed with distilled water with w = 1.4 LL, placed into cell consolidometer, and given a light vibration. |
Po =20 ΔP = 60 |
100 x 4 | 115 x 10 Recta- ngular |
- | 2.5 | 1.3 | ||||||||||
The soil sample to be tested in the soil tank is divided into two types, i.e. disturbed and undisturbed. Because it is difficult and costly to make a sample that is not disturbed in a large scale, most laboratory tests use disturbed soil samples, employed among others by Sharma and Xiao (2000) [3], Chai et al., (2013) [28], and Sengul et al., (2016) [33]. On the other hand Rujikiatkamjorn et al., (2014) [29] used a relatively large of undisturbed sample with the aim of capturing more realistic smear zone characteristics within the intact soil structure, whereas Indraratna et al., (2015) [30] used a comparatively small, undisturbed sample directly from the field for oedometer testing. See Table 2 for more complete conditions and results of 17 previous laboratory studies on the smear zone.
The testing normally starts from the sample preparation stage. The sample preparation is carried out by mixing the soil with water until saturated, putting it into a consolidometer cell, extracting trapped air, and providing a pre-consolidated compression. This stage is followed by the PVD or sand drained (SD) installation. The insertion of PVD (or SD) utilized a round or rectangular mandrel with a size smaller than the actual size. Also, the insertion speed in the laboratory is usually smaller than that in the field. Finally the consolidation stress representing the preloading is given. Based on the results of consolidation happening in the lab, the determination of the smear zone characteristics can be done. Columns 10-11 in Table 2 shows the results of the 17 previous laboratory on the characteristics of the smear zone composed mainly of soft soils.
5. FIELD DATA vs LABORATORY RESULTS
With reference to Tables 1 and 2, the extent ratio s’ in the smear zone varies between 2.0-5.0 in the field using back calculation and 2.0-6.3 in the lab using laboratory apparatus. On the other side the permeability ratio κ varies between 2.0-13.8 in the field using back calculation and 1.03-3.13 in the lab using laboratory apparatus.
It appears that the extent ratio s’ resulting from both methods, field data back calculation and laboratory testing, yields comparable range. On the other hand the permeability ratio κ resulting from the field data back calculation reveals a noticeably greater range if compared with that resulting from laboratory testing. The greater range of κ values in the field indicates that the level of disturbance in the ground varies greatly between locations. Also, the discrepancy in κ ranges implies that the laboratory testing can hardly model the high level disturbance of field conditions.
6. DISCUSSION
6.1. Soil Conditions Before PVD Installation
Soil samples are usually taken to the laboratory to determine the basic soil properties before PVD installation. See column 4 in Table 2 for the basic soil properties used in the lab.
Refering to the same soft soil prior to the PVD installation, Bo et al., (2001) [39] compared the values of permeability and consolidation coefficients (k and cv or ch respectively) from laboratory testings with those from field methods. They found that the corresponding values from laboratory results were noticeably lower than that from field testing. Similar results were previously reported by Balasubraniam et al., (1995) [40].
Chai and Miura (1999) [12] suggested that laboratory testing was the correct way to determine the value of ks for the smear zone, but the permeability coefficient value k determined in laboratory before PVD installation would typically be lower than that in the field, resulting in smaller values of κ. Later Chu et al., (2002) [41] used Rowe consolidation cells in the laboratory to determine the coefficient consolidation values of ch and cv; however, they concluded that the resulting ch and cv values could not represent the natural conditions of the soil. In short it should be pointed out that the important parameters of the soil including ch, cv, and k determined in the laboratory can hardly represent the soil's natural conditions due to the inherently complex soil structures which cannot be represented within small specimen dimensions.
6.2. Soil Conditions During and After PVD Installation
6.2.1. Land preparation for PVD Installation
Land clearing and stripping is done in the field to clean the soil surface and remove layers of humus and other organic materials. A layer of sand blanket as thick as 0.5 m up to 1 m is then compacted on top of the soil surface. During the operation of PVD installation, the ground receives the moving load of the PVD rig; hence, the near top soil would be disrupted. This condition can hardly be modeled in the laboratory testing.
6.2.2. Installation Depth of PVD
Due to its very limited depth of less than 1 m, soil in the laboratory receives a comparatively small amount of disturbance forces during PVD installation. On the other hand, Indraratna et al., (2015) [30] stated that the ground in the field gets distorted by the shear stress due to the PVD insertion. They also stated that the degree of distortion is more significant when the installed PVD gets longer. In this regard, laboratory testing is incapable of modelling the disturbing effects in the soil model caused by the depth of installation in the field. It should be noted that in the previous study sites, the depth of installation, indicated in column 3 in Table 1, varies between 8.0 m and 50.0 m dependent upon the field conditions, leading to the variation of the smear zone characteristics.
6.2.3. Distance Between PVD
Bo et al., (2003) [20] found that the extent ratio s’ = 4 up to 7; then, for a PVD with an equivalent diameter of dw = 66 mm, the smear extent ds = 480 mm up to 528 mm. Consequently PVDs installed with an interval of less than 1.0 m will start to have the interacting smear zones in which their disturbance effects on the permeability are unusually large, leading to a lower value of horizontal consolidation coefficient ch. Balasubraniam et al. (1995) [40] and Chu et al., (2002) [41] reported the phenomenon of overlapping smear zones which cause the horizontal consolidation ch to be less than the vertical consolidation cv, a condition at variance with the expectation. Walker and Indraratna (2007) [42] performed an analytical solution to assess the effect of overlapping smear zones and indicated that the critical, minimum effect radius was 0.55 rs to 0.60 rs. The disturbance conditions due to the overlapping smear zones of the closely installed PVDs cannot be investigated in the laboratory since only single PVD has so far been modelled. At the previous study sites, the distance between PVDs, indicated in column 6 in Table 1, varies from 0.85 m to 3.0 m affecting the variation of the smear zone characteristics.
6.2.4. Stiffness of Soil
According to Sathananthan and Indraratna (2006) [23] and Sengul et al., (2016) [33] the extent ratio s’ depends on soil stiffness. For more rigid soils, s’ is greater than that for less rigid soils. With respect to the SPT values, the stiffness of the soil is not the same at every location and depth. Hence, the vertical variation in soil stiffness results in the variation of the smear extent in the vertical direction. Due the limited sample sizes, the soil stiffness variation is barely reflected in the laboratory.
6.2.5. The dimension, Shape and Type of Mandrels
The installation of PVD in the laboratory is generally performed using a mandrel that is reduced in size. In the field the commonly used sizes of mandrels are 120 mm x 60 mm for rectangular shape and 120 mm x 39 mm or 145 mm x 90 mm for rhombic shape. The use of large mandrels serves to maintain the rig balance when installing PVD on thick soft soil layers. Sathananthan and Indraratna (2006) [23] affirmed that the extent ratio s’ depends on the dimensions of the mandrel used.
Bergado et al. (1991) [6] did experiments at a trial embankment by installing PVDs using large and small mandrels and indicated that the resulting dissipation of pore pressures were faster in locations using smaller mandrel. Their extensometer data showed slightly lower rates of settlement occurring in areas that use larger mandrels. Also, their back calculation at locations that use large mandrels yielded smaller horizontal consolidation coefficient ch values than those at locations using small mandrels.
It should be noted that trial embankment is costly but the smear zone parameters resulting from it better reflect the physical conditions of the field. Hence if fund is permitted, trial embankment is recommended to measure the settlement and excess porewater pressure to enable the back calculation method to search for the more accurate extent ratio s’ and permeability ratio κ.
In relation with the shape effect, Bo et al., (2003) [20] explored that there are four shapes of mandrel namely rhombus, rectangle, square and circle and stated that the rhombus resulted in the least disturbance to the soil. In addition they indicated that the static rig used to drive PVD into the ground caused less interference if compared with the vibration rig. Likewise Tran-Nguyen and Edil (2011) [26] concluded that the size and the shape of mandrels were important factors affecting the value of s’.
The dimension, shape and type of mandrel cannot be modelled precisely in the laboratory. At the previous study sites, the dimensions and shapes of the mandrels used in the field and in the lab vary as indicated in column 7 in Table 1 and in column 8 in Table 2, consecutively.
6.2.6. The Speed of PVD Installations in the Field
The installation of PVD in the laboratory is normally performed at low speeds, ranging from 0.5 to 20 mm/s. Sathananthan and Indraratna (2006) [23] stated that the extent ratio s depended on the speed of the PVD insertion. In contrast Rixner et al. (1986) [5] stated that PVD was installed in the field at a speed of 150 up to 600 mm/s. Hence the ground disturbance in the field is greater than that in the laboratory. In Tables 1 and 2 the speeds of PVD installation are given in column 10 for field and in column 9 for laboratory, respectively.
6.2.7. Use of Reconstituted Soil Samples
Liu and Carter (2000) [43] discussed how the behavior of soil structures of the original soils was different from that of the reconstituted soils. Tran-Nguyen and Edil (2011) [26] who used reconstituted samples revealed that the extent and permeability ratios measured in their laboratory results were at the lower limit reported in the literature. These may occur because the soils were very disturbed and had no structure, thus less susceptible to disturbance.
The laboratory testing using undisturbed soil samples was done by, among others, Rujikiatkamjorn et al., (2014) [29] who found that permeability reductions were almost twice as much as those using disturbed soil. Bo et al., (2003) [20] suggested that the smear zone could become larger in undisturbed soils due to the destruction of the soil structure. In any case the condition of the soil in the field is normally not disturbed, leading especially to the higher values of the permeability ratio κ.
6.2.8. Total Height of Embankment
Total height of embankment is directly responsible for the total working consolidation stress in the soil. Sharma and Xiao (2000) [3] and Sathananthan and Indraratna (2006) [23] confirmed that the permeability ratio κ would decrease with the increasing pressure of consolidation. Most recently Sengul et al., (2016) [33] reassured the decrease of kh/ks and kh/kt in smear and transition zones with the increased consolidation stress. The variation of the total height of embankment in the previous study sites is given in column 9 in Table 1, ranging from 1.5 m up to 8.0 m.
In the laboratory testing the total height of embankment is applied using the consolidation stress as indicated in column 6 in Table 2. Referring to the table, the consolidation stress ranges from 47.8 kPa to 1102 kPa indicating quite a large variation in terms of the total embankment heights which are modelled in the lab.
6.2.9. The Ranges and Classification of s’ and κ Values
As mentioned earlier, the extent ratio s’ values vary between 2.0 – 5.0 and between 2.0 – 6.3 based on field data back calculation and laboratory testing, consecutively. On the other hand, the κ values vary between 2.0 - 13.8 and 1.03 – 3.13 based on field data back calculation and laboratory testing, consecutively. It can be seen that the ranges of s’ values from both methods are relatively close since the key factor, the soil stiffness, is not disturbed much in both cases. In contrast, the range of κ values from field data is significantly larger than that from laboratory testing due to the complexity and high level of disturbance in the field.
The range of the s’ values can be classified as follows:1<s’<2 low, 2≤ s’ <4 moderate, and 4≤ s’<7 high. It is found that the values of s' based on field data back calculation and laboratory test results are mostly in the moderate range.
The range of κ values can be classified as follow:1< κ<4 low, 4≤ κ <7 moderate, 7≤ κ<10 high, and 10≤ κ<14 very high. It is found that the values of κ based on field data back calculation are mostly in the high to very high ranges, while the κ values from laboratory test results are mostly in the low range.
7. A CASE STUDY
The position of the case study is at the location of the multi purpose container yard in Kuala Tanjung Port which is is located on the east coast of North Sumatra, Indonesia, fronting the Strait of Malacca. Fig. (2) shows the 13.5 ha of the embankment area of the case study site taken during preloading in June 2017.

The soil investigation was carried out using a machine drill, SPT, undisturbed and disturb samplings, DCP, and laboratory testing. From the results of the soil investigation it is known that the basic soil layer is composed of soft clay and very soft clay as thick as 10 m, with SPT ≤ 2. This clay layer sits above a sandy clay layer having a medium consistency of 7 m thick with 4≤SPT≤5. This sandy clay layer is located above a dense sand layer of 3 m thick with 10≤SPT≤30, below which a very dense sand layer of 10 m thick rests with SPT≥60.
A geotextile separator is used over the 13.5 ha of the embankment area to separate the base ground with the embankment material. The data related to the PVD work in the case study site can be seen in the last row in Table 1. The geotechnical instruments used for the analysis encompassed 7 piezometers, 7 water standpipes, 44 settlement plates, and 8 inclinometers. The total height of the embankment, which has an average of 5.2 m, was achieved gradually in 14 stages as indicated in Fig. (3).
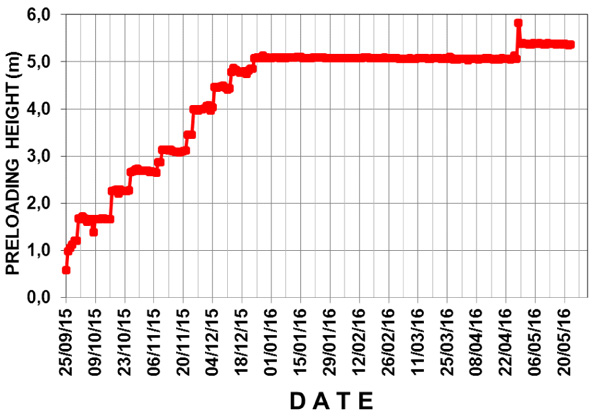
The consolidation induced settlement is calculated using the 1-D consolidation with the load distribution following the 2V:1H ratio and ch=1,35 cv.The degree of consolidation of the embankment is estimated by taking the smear zone effect into account and ignoring the well resistance.
The characteristics of the smear zone are determined through the back-calculation method using time dependent settlement data obtained from the case study site (Fig. 4). For the case of constant permeability in the smear zone, the settlement data are fitted with Eq. (1) using the parameter m of Eq. (4). For the case of parabolic permeability in the smear zone, they are fitted with Eq. (1) using the parameter m given by Eq. (5). Lastly, for linier permeability in the smear zone, they are fitted with Eq. (1) using the paramater m given by Eq. (6).
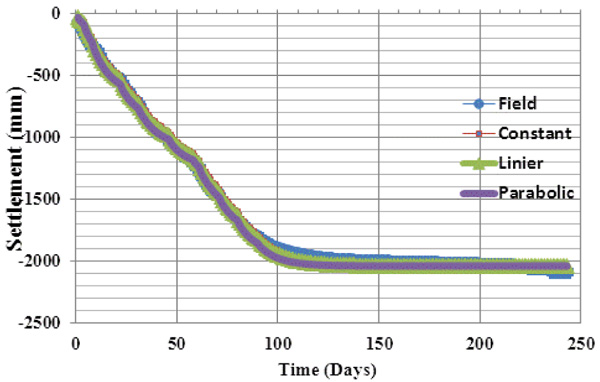
Plotted against the field settlement data in Fig. (4), the results of the consolidation for the three permeabilities are obtained using the value of s’ = 3 and κ = 7. If the results in the figure are checked in detail, it can be seen that the discrepancies appear to be significant on days 85 up 135. However, the largest discrepancy is found to be with the parabolic permeability, followed by the linear and the constant permeabilities in a decreasing order. It is noteworthy that the extent ratio s’ = ds/dm= 3 is the value suggested by Chai and Miura (1999) [12] for locations with no test data. Meanwhile the value for permeability ratio κ=(kh/ks)=7 can be considered as a high representative value that reflects the level of disturbance in the soil during PVD installation.
CONCLUSION
In this study we have documented and evaluated the values of smear zone parameters, namely the extent ratio s’ and the permeability ratio κ, resulting from field investigation and laboratory testing. The assessment on the causes of the variation of the values of the smear zone parameters is made particularly with relation to the different conditions in the field and in the laboratory. A case study is given here to illustrate the procedure to estimate the values of both parameters by field data back calculation. The concluding findings can be summarized as follows.
Smear zone parameter values are quite different in accordance with their locations. With reference to the results of the previous studies it is found that the extent ratio s’ values vary between 2.0 - 5.0 and between 2.0 - 6.3 based on the back calculation and laborary testing, consecutively. On the other hand, the permeability ratio κ values based on the field data back calculation range from 2.0 to 13.8 which are quite large if compared with the κ range from 1.03 to 3.13 based on laboratory testing.
Three causes of the s’ and κ variations are suggested here. First, the laboratory testing is unable to model the complexity of field conditions. Second, there are no standards established to be used as references in the laborary testing. Third, the level of disturbance in the field is much greater than that in the laboratory testing and differs at each research location.
If fund is permitted, it is recommended that a trial embankment be applied using the same methods, materials and equipment that will be used on the actual embankment. Then smear zone parameter values will likely be obtained with a better accuracy for the real application of PVD.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICTS OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors gratefuly acknowledge the financial assistance from the University of Sumatera Utara (Research Contracts Fiscal Year 2018, Number: 2590/UN5.1.R/PPM/2017 dated March 16, 2018). Appreciation is given to PT. Prima Multi Terminal which provided the authors with data for the case study. The contribution from Nurhayani Simamora in typing and formating the paper is also appreciated.


