All published articles of this journal are available on ScienceDirect.
Seismic Performance of Steel Moment Frames Containing Concentric Bracing Equipped with Shape Memory Alloys
Abstract
Background:
A building’s stability is a critical design element that structural engineers must understand. Utilization of Shape Memory Alloys (SMAs) in steel structures can significantly diminish seismic residual deformations, which will facilitate postseismic retrofitting.
Objective:
The aim of the present study was to evaluate the seismic behavior of 7-story and 15-story steel frames with a moment frame system having a chevron concentric brace equipped with Shape Memory Alloys (SMAs). Braces containing various amount of alloy (including 20%, 40%, 60%, 80%, and 100%) were applied to study the effect of SMAs on structural performance. Relatively persistent displacement of the structure as well as its relative maximum displacement under the earthquake imposing on frame models, were investigated using non-linear dynamic analysis by OpenSees finite element software. The earthquakes were in near- fault nine accelerographs, which involved various maximum accelerations.
Results:
Results indicated a reduction in relatively persistent displacement using 20% SMAs in braces. Additionally, more amount of alloy resulted in less relative displacement as compared to steel braces.
Conclusion:
Applying SMAs brace showed a reduction in persistent structural displacement in any type of frame. Furthermore, adding more than 20% SMAs to the brace, resulted in a decrease in structural displacement.
1. INTRODUCTION
Smart engineering systems due to controlling structure vibration response, partial absorption of vibration energy, and reduced earthquake forces on structures have been developed [1]. Shape Memory Alloys (SMAs) increasingly developed in recent decades played a key role in smart systems development. These smart materials consist of physical and mechanical components, which are applied in engineering applications [2]. Nevertheless, the performance of steel bracing frame, low flexibility and energy dissipation regarding brace buckling failure, asymmetric behavior in tension and pressure of brace member, and member joint failure are considered as structural weak points in recent earthquakes [1]. Buckling restrained braced frames have been offered as a new bracing system to overcome these problems. Large persistent displacement following an earthquake, however, has never been solved, but alternative strategies using SMAs are recommended.
In previous decades, Clark et al. [3] studied shape memory systems in controlling steel multi-story buildings in which wire rings were integrated with out of alignment braces. The results indicated that the drift reduced around 50% and energy absorption by the frame decreased around 15% in comparison with the frame, which did not involve a system. Subsequently, Seelecke et al. [4] investigated damper geometry effects, which were characterized by a superelastic feature of SMAs on the dynamic response of the one-degree freedom model as a building subjected to an earthquake. They proved that SMAs corrected wire diameter resulted in optimal vibration performance. Also, Han et al. [5] studied the performance of eight damper systems constructed in shape memory wires and steel ones located in a two-story steel frame diagonally.
Experimental results represented a more sudden reduction in vibration in an SMAs-controlled frame than no controlled one. Moreover, the maximum displacement of the controlled frame was only 15% of the uncontrolled one [5]. Auricchio et al. [6] investigated the seismic performance of a steel frame of three-story and six-story buildings, which were enforced by various shape braces. The bracing systems consisted of a traditional buckling restrained brace and a superelastic Nitinol one. The SMAs bracing system showed a vibration reduction against seism [6]. Motahari et al. [7] compared various innovative systems of SMAs dampers and buckling restrained bracing ones. Damage index was applied to compare multi-story building frame dissipation due to earthquakes. Results illustrated that SMAs damper systems significantly decreased structural vulnerability while represented some restrictions on non-structural ones. Researchers indicated that SMAs bracing systems had large ductility, good energy dissipation, effective performance mechanism, and high self-centered and stiffness in small displacement. Nevertheless, as buckling restrained brace systems have wide energy dissipation capacity, hybrid systems in bracing structural frames were produced to combine energy absorption and self-centered characteristics effectively, which may be useful when a strong earthquake occurs [7]. Ma et al. [8] provided an SMAs innovative damper in spring consisting of memory alloy wires, which was based on friction. Its performance was designed on energy dissipation and reversibility. Memory alloys increased energy dissipation capacity and restoring force [8]. Yang et al. [9] investigated the seismic performance of memory alloys bracing system in terms of reversibility parameter and energy absorption. SMAs systems were evaluated using three models and two situations. Non-linear and pushover dynamic analyses indicated that enjoying a good reversibility capacity, the energy dissipation capacity of the bracing system and buckling bracing system were the same [9]. Miller et al. [10] experimentally studied a hybrid system, which consisted of a normally buckling restrained brace component and Nickle memory bars with provided and additional energy dissipation, respectively. The results represented high resistance of brace against earthquake, stable hysteresis with remarkable energy dissipation, and reversibility. In addition, it was revealed that even if buckling restrained brace core failed, it could bear large loads due to shape memory bars added. Asgarian and Moradi [11] investigated the seismic performance of an SMAs steel bracing frame, whose brace had different shapes. Dynamic response of the SMAs brace frame showed an energy dissipation capacity, corresponding to buckling restrained brace. Furthermore, results indicated that hysteresis of these alloys during loading cycles under great transformations enabled to reduce maximum drift by 60%. Jani et al. [12] studied the performance of SMAs in a widespread investigation. SMAs, which were subjected to certain factors including temperature or magnetic changes, could maintain their shape, so due to some peculiar characteristics have drawn attention [12]. Hooshmand et al. [13] studied the performance of a simple three-story frame containing concentric cross brace. They equipped cross bracing with SMAs then evaluated its performance.
Combining structure bracing and various percent of SMAs as well as imposing earthquake load, they compared persistent displacement and energy dissipation of the structures. They applied six types of braces consisting of various percent of SMAs; steel brace, braces comprising 20, 40, 60, 80 and 100% of SMAs. Results indicated that when SMA percent was increased the persistent displacement of the structure decreased. A maximum reduction in displacement occurred when 20% of SMAs were added to. More SMAs addition resulted in a decrease in the reduction of persistent displacement [13]. Menna et al. [14] investigated SMAs functions in civil engineering and mentioned that SMAs possessed some physical and mechanical properties including resistance against corrosion and fatigue, reversibility and high capacity on energy dissipation [14]. Gao et al. [15] suggested an experimental model to evaluate the SMAs seismic effect.
Regarding remarkable reversibility, these alloy showed a high capacity in seismic performance. A system consisting of an SMAs ring with reversibility and energy dissipation capacity was investigated, and its performance evaluated by static and finite elements loading analysis using Abaqus software. Experimental results showed the reversibility and energy dissipation capacity of the system [15]. Sultana et al. [16] examined the seismic performance of an SMAs moment frame. The optimum locations of SMAs in the moment frame joints to improve seismic performance ie, maximum displacement and persistent displacement, were investigated [16]. Vafaee et al. [17] evaluated the seismic performance of SMAs bracing frames. Results indicated that SMAs play a key role to control the vibration of enforced frames. They also showed a high performance in displacement reduction and persistent displacement [17]. Qiu et al. [18] compared the seismic performance of buckling restrained brace frames with SMAs ones. Results demonstrated duckling restrained braces affected energy dissipation, but had no effect on the reduction of persistent displacement. SMAs, however, indicated no or little deformation under cyclic loading showing reversibility and remarkable energy dissipation [18]. Hou et al. [19] studied the impact of hysteresis properties of SMAs on the seismic behavior of coaxial brace frames. Non-linear records were analyzed to evaluate the seismic performance of the structures under usual designed earthquakes. Analytical results demonstrated structures provided the proposed performance and seismic demands [19]. Wang et al. [20] experimentally investigated the cyclic behavior of SMAs bars with reversibility under stress and tension. Reversibility and energy dissipation were evaluated in loading protocol. Results demonstrated satisfactory and stable hysteresis loops in multiple cycles attained under stress and tension loadings. Moreover, the shape memory bar showed remarkable reversibility independent of stress and loading protocol [20]. Dutta et al. [21] studied the vibration response of a two-story steel structure, which was equipped with SMA. The results showed a significant reduction in vibration in a brace when using SMA. Sultana et al [22] studied the seismic performance of steel frames equipped with SMA. They explored that using SMA braces in a certain location significantly reduced residual drifts. Mahmoudi et al. [23] investigated the seismic performance of X-knee-braced frames equipped with SMA. First, they modeled 3 frames in OpenSees. By placing the super elastic elements between beam-column joints and knee members, they examined some structural properties. Then they performed pushover analyses. The results showed that the permanent displacement of structures is reduced when these elements are used.
Nazarimofrad et al. [24] studied the seismic performance of steel braced frames equipped with SMA. They reported that using buckling-restrained braced frames made of hybrid steel and SMA can increase the ductility of the structure and decrease residual displacement of the structures. Mirzai et al. [25] investigated the performance of eccentrically braced frames equipped with SMA. They performed a numerical analysis for a nine-story steel frame building using OpenSees. Time history analysis indicated that the self-centering behavior of the proposed system was better as compared to the eccentrically braced frame. Qiu et al. [26] studied the scald self-centering steel frame with novel SMA braces that used superelastic Ni-Ti wires. Their experimental results showed that the SMA brace could withstand strong earthquakes. They also indicated that the steel frame was subjected to limited damage and zero residual deformation. Dong et al. [27] studied seismic responses of steel frame structures with self-centering energy dissipation braced on SMA cables. They carried out numerical studied on seismic responses of the frames using OPenSees. First, they experimentally investigated the mechanical properties of SMA cables. The results showed the excellent super elastic property of the cables. Numerical results also demonstrated that self-centering energy dissipation brace can reduce the drift ratio of the structures. Fang and Wang [28] studied seismic performance of steel frame buildings with SMA-based self- centering bracing systems using a probabilistic method. Their case study building was a four-story steel frame building that was characterized until collapse in their previous research. After developing numerical models and conducting nonlinear static analyses, they reported that steel frames with bracing systems showed a lower probability of reaching a damage stage level compared to a similar steel moment resisting frame.
The effect of SMAs adjoin to chevron braces in various multi-story structures containing moment frames subjected to the earthquake has not been comprehensively studied yet. Thus in this research, such an effect is evaluated. Two 7-story and 15-story structures containing braces of 20, 40, 60, 80 and 100% SMAs mixed with steel were studied. Following modelling, nine near field earthquakes as accelerographs containing various maximum acceleration imposed on the structures and persistent displacement of the structure were studied.
2. INNOVATION AND SIGNIFICANCE OF RESEARCH
Having a particular property, SMAs may retain their primary shape after the load is removed. In fact, when the temperature of the alloys rises, it results in a full reverse of persistent strain, which in turn, is due to mechanical loading and unloading [1]. These materials possess peculiar properties; they play a significant role in controlling engineering structures. Although in previous studies, the effect of SMAs was studied on simple building frame systems (building frame with concentric brace), but such an effect was not studied on structures containing hybrid systems (with moment frame and concentric brace). Therefore, in this research the effect of SMAs on the behavior of hybrid frames systems of 7-story and 15-story was studied. Various percent of the alloys in braces in different frames under near field earthquakes and the optimum percent of the SMAs to minimize persistent displacement was also studied. It is noteworthy that the behavior of structures under various accelerographs of near field earthquakes, which has been studied in this research, has no record before.
3. MATERIALS AND METHODS
3.1. Behavior of SMAs
The functional properties of SMAs, in general, belong to their phase change. Temperature change particularly results in reversibility and super elastic feature as follows:
3.2. SMAs
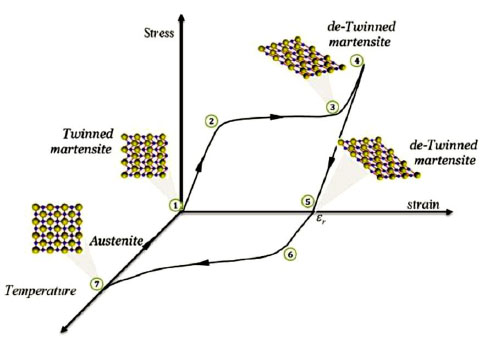
Fig. (1) illustrates the shape memory effect as a schematic in which tension, strain and temperature are shown. The materials start at a certain temperature and zero tension. As the tension arises, materials behavior develops linear elastically first (slope 1-2) then following plastic deformation, they develop in almost stable tension on the contrary to plastic deformation (slope 3-2). Nevertheless, SMAs deformation is saturated and more overload created a linear elastic branch (slope 4-3). After unloading, remained deformation (slope 5) can be reversed by heating materials at a certain temperature, but no load (slope 7-6). Finally, once materials are cooled down to the early point they may reverse completely.
3.3. Super Elastic Property
Once SMAs single wires are activated by heat, they may create high-pressure tension under finite circumstances. Tensions up to 800 m Pascal are attainable. When SMAs are deformed and limited in low temperature, increased temperature results in phase change, and recovery tension in materials tends to return to its original shape. Cooling along with tension, unpaired Martensite phase is corrected and recovery tension releases completely or partially. The SMAs require temperature change; on the contrary, the quasi-elastic effect is the temperature in nature and enjoys energy saving potential. Particularly, SMAs super elastic behavior belongs to tension-based changes, which occur in more than AF. In fact, the alloy may deform elastically at a normal level more than imposed load in the Austenitic phase. Peculiarly, Nitinol is elastically strained around 8% while most of the metals can elastically strain less than one percent. Imposed load turns unpaired Austenite to Martensite one. Following unloading, the Martensite phase becomes unstable and turns to the primary Austenite phase. Removing load, the full strain is recovered. Super elastic property in tension-strain areas is illustrated in Fig. (2) [1].
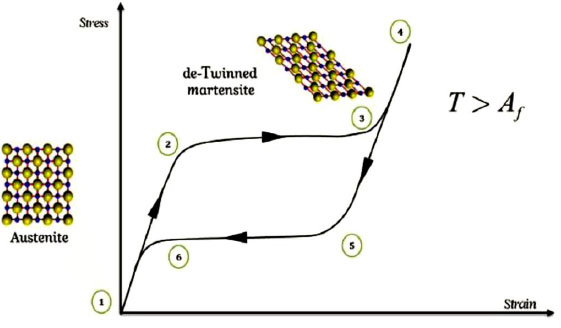
Macroscopic materials are Austenitic first (point 1). During loading, critical tension reaches to phase change (point 2). Materials are directly turned to unpaired Martensite (level 3-2). In the complete phase, more loading causes elastic deformation from unpaired Martensite (slope 4-3). The austenite phase is stable only at high temperatures and in the absence of tension, so during the loading, critical tension is ready for reverse phase change, and macroscopic deformation is recovered (level 6-5). There is a small hysteresis loop between loading and unloading which refers to as super elastic property.
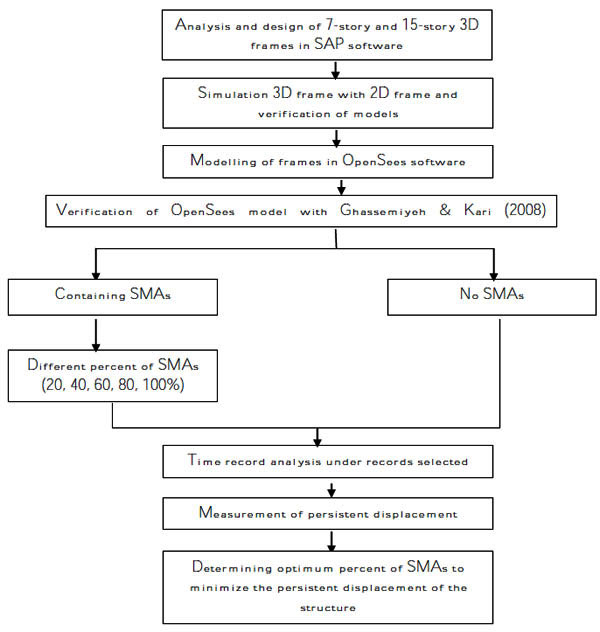
4. RESEARCH FLOWCHART
As indicated in the flowchart (Fig. 3), the first step consisted of designing 3D structures containing hybrid system (moment frame and concentric brace) of 7-story and 15-story structures using SAP software. Then, a 2D frame was selected from the 3D structure and the former was simulated with the latter using pushover analysis. The 2D frame model was then verified in OpenSees software using Ghassemiyeh and Kari [29] model. In the next step, considering SMAs bracing and free SMAs bracing, 2D frames were modelled. The percent of SMAs used in the research was 20, 40, and 100%. Frames were then subjected to various near field accelerographs. Following the earthquake imposed, persistent displacement of the structure was measured. Comparing persistent displacement of the frames in different circumstances, the optimum percent of SMAs was determined to minimize the displacement.
5. MODELLING
As mentioned above, OpenSees software was used to model SMAs. Model verification, properties of behavior model of SMAs and parameters used, geometric features of the model, section used and characteristics of imposed earthquakes in the model for steel and SMAs were as follows:
5.1. OpenSees Software and the Elements
OpenSees is software for non-linear analysis of open source structures, which consists of a full body of elements, materials and different analysis procedures. The research elements are non-linear ones (non-linear Beam Column). Non-linear materials model (Steel 01) was used to model steel elements in software. Materials of SMAs were modelled using SMAs uniaxial aggregate model of the software [30].
5.2. Verification
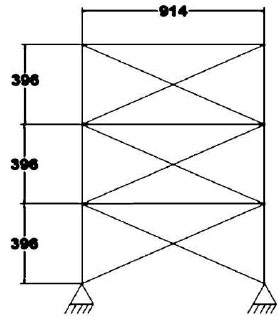
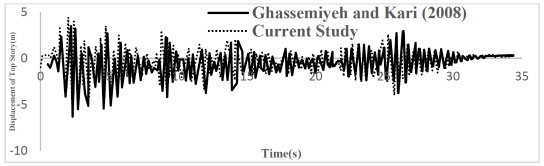
To verify the model, the behavior of the OpenSees-based model was compared with Ghassemiyeh and Kari [29] 3-story bracing structure AIMS-based model. The geometry model and section utilized are indicated in Fig. (4) and Table 1. SMAs bracing is used in these models.
| Number of Floors | Sections Used for Bracing | Sections Used for Beams | Sections Used for Columns |
|---|---|---|---|
| 1 | HSS 8x8x0.5 | W18x46 | W12x106 |
| 2 | HSS 6x6x0.5 | W18x46 | W12x106 |
| 3 | HSS 5x5x0.375 | W18x46 | W12x106 |
| Research | Persistent Displacement (meters) |
|---|---|
| Ghasemiyeh & Kari (2008) | 0.3 |
| Current research | 0.27 |
Structural response in Ghassemiyeh and Kari [29] modelling and OpenSees software under earthquake is illustrated in Fig. (5). Also, persistent displacement in these two models is shown in Table 2 which are equal approximately.
5.3. Behavior Model of SMAs
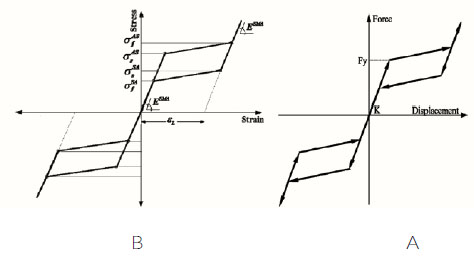
SMAs models have drawn much attention in recent decades. Several constructed models have been suggested by researchers to evaluate SMAs behavior. Here, Fugazza [31] model was applied to evaluate SMAs super elastic behavior. Tension- strain diagram according to Fugazza [31] model is shown in Fig. (6).
Models parameters which consist of Austenite tension start to Martensite (
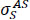 ), Austenite tension end to Martensite (
), Austenite tension end to Martensite (
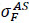 ), Martensite tension start to Austenite (
), Martensite tension start to Austenite (
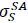 ), Martensite tension end to Austenite (
), Martensite tension end to Austenite (
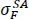 ), elastic modulus for Austenite and Martensite
), elastic modulus for Austenite and Martensite
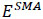 and super elastic strain length
and super elastic strain length
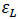 are illustrated in Table 3.
are illustrated in Table 3.
| Parameter | Value |
|---|---|
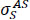 |
414 MPa |
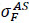 |
550 MPa |
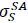 |
390 MPa |
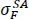 |
200 MPa |
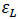 |
3.5% |
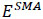 |
27579 MPa |
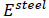 |
200000 MPa |
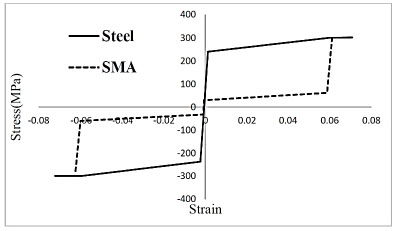
Fuggaza [31] model used for SMAs and the model applied for steel are shown in Fig. (7).
5.4. Geometry Properties of the Model
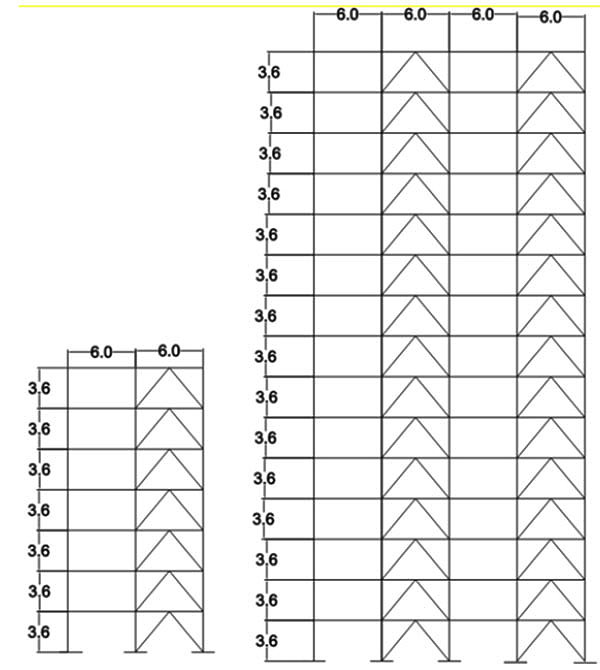
To evaluate the SMAs effect on braces, two 7-story and 15-story structures were modelled in SAP2000 in virtue of regulation concerned. The geometry of the 7-story and 15-story models consisted of two and four frames with 6 m height respectively and each floor had 3.6 m height. They are illustrated in Fig. (8).
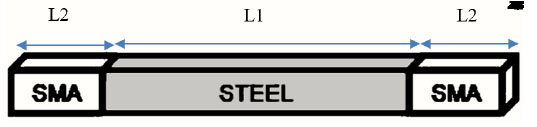
The geometric placement of SMAs and steel bracing is represented in Fig. (9). As the Figure shows, SMAs are placed at two ends. As the SMAs portion increases the steel portion decreases reversely.
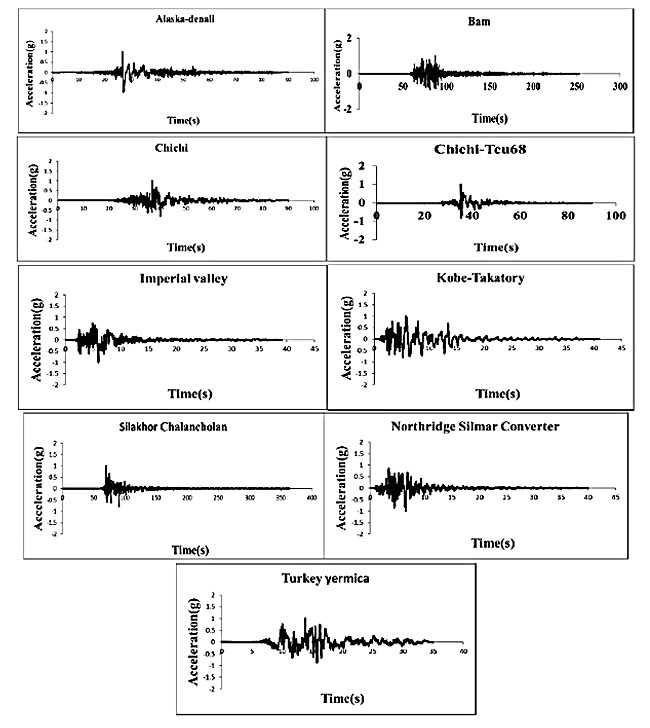
| No | Earthquake | Arias Intensity |
Mean Period | Predominant Period | Significant Duration | Duration | PGA |
|---|---|---|---|---|---|---|---|
| 1 | Alaska-Denali | 19.43 | 1.5233 | 0.94 | 21.55 | 89.995 | 0.32g |
| 2 | Bam | 53.64 | 0.7087 | 2.16 | 37.297 | 252.871 | 0.59g |
| 3 | Chichi-1012 | 15.47 | 0.9641 | 0.90 | 26.49 | 89.995 | 0.44g |
| 4 | Chichi-tcu68 | 10.31 | 1.5110 | 0.42 | 12.475 | 89.995 | 0.56g |
| 5 | Imperial Valley Array 6-2 | 9.10 | 1.2737 | 0.24 | 8.49 | 39.03 | 0.43 |
| 6 | Kobe | 23.26 | 1.131 | 1.22 | 11.34 | 40.95 | 0.61g |
| 7 | Northridge Silmar Converter | 11.92 | 0.7439 | 0.22 | 7.525 | 39.995 | 0.49g |
| 8 | Silakhor | 28.81 | 1.8228 | 1.52 | 56.34 | 363.5 | 0.447g |
| 9 | Turkey Yermica | 18.56 | 1.2424 | 0.52 | 15.335 | 34.995 | 0.26g |
 |
6. RESULTS AND DISCUSSION
To compare displacement of the top floor containing full steel brace and various SMAs brace, displacement diagrams in terms of time are represented in Fig. (11) for steel brace, 20% SMAs brace and 100% SMAs brace for 7-story and 15-story frames, using three accelerographs ie, Imperial Valley, Bam and Alaska- Denali. Obviously, 20% of memory alloy bears showed less persistent displacement than steel and 100% SMAs ones. Another conclusion is that maximum displacement during the earthquake occurs in 100% SMAs.
The results of persistent displacement due to the addition of various percent of SMAs for 7-story and 15-story structures are displayed in Fig. (11). Regarding process of persistent displacement in Figs. (12 and 13), in most earthquakes (Alaska-Denali, Bam, Chichi-tcu 68, Northridge Silmar Converter, Silakhor, Turkey, Yermica), the addition of SMAs to braces first resulted in reduction in persistent displacement (up to 20% SMAs), but further addition of SMAs resulted in an increase in displacement. The addition of SMAs in the Kobe earthquake resulted in an increase in persistent displacement, which was on the contrary to other earthquakes. Reasons may belong to maximum acceleration and high earthquake maximum period. Addition SMAs percent in Chichi-1012 and Silakhor earthquakes resulted in a reduction in persistence displacement which may contribute to a low earthquake maximum period.
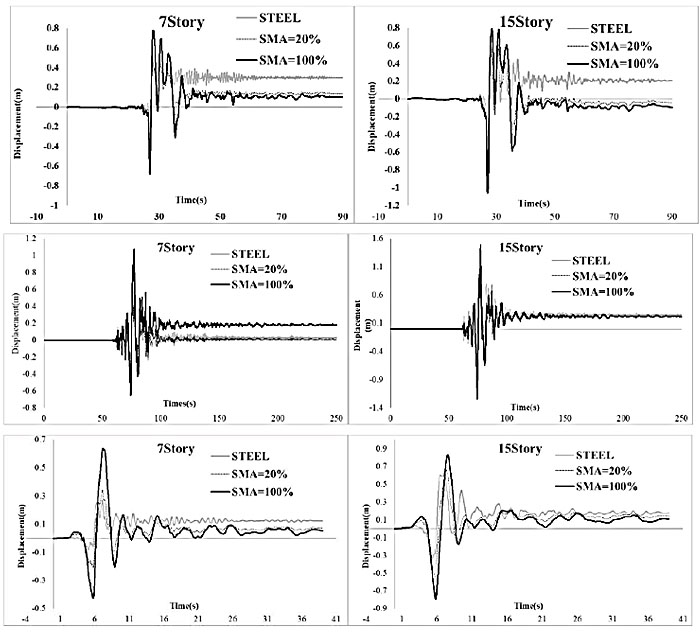
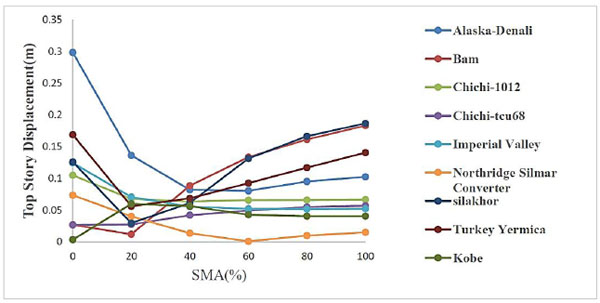
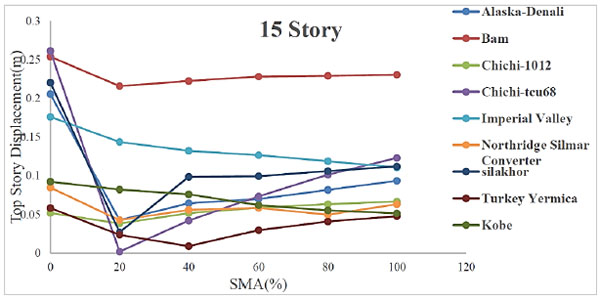
In earthquakes such as Bam, Silakhor and Kobe- in which PGA, significant duration and Arias intensity were greater than others - an increase in SMAs percent caused more increase in persistent displacement in the structure. This was because of a reduction in structural stiffness that was due to SMAs addition. So, an increase in SMAs percent in structure resulted in stiffness reduction, and a strong earthquake caused greater persistent displacement.
Finally, SMA addition to braces of 7-story and 15-story structures up to 20% resulted in reduction in persistent displacement against earthquakes. Optimum use of SMAs was about 15%– 25%. More SMAs addition up to 100% resulted in more structural persistent displacement. It might contribute to less SMAs elasticity modulus versus steel one. More than 40% increase of SMAs to brace resulted in total reduction in structures stiffness.
CONCLUSION
The effect of SMAs addition on the behavior of two 7-story and 15-story structures with chevron brace was evaluated by OpenSees software. SMAs value in braces was 0%, 20%, 40%, 60%, 80% and 100%. The structures’ behavior was studied under the effect of nine accelerographs, and then persistent displacement of the top floor under various earthquakes was evaluated. Results indicated a reduction in persistent displacement when adding SMAs up to 20%. Values more than 20% of SMAs resulted in more persistent displacement. This situation did not apply to Kobe, which might be related to maximum acceleration and high earthquake maximum period. Additional SMAs percent to braces in Chichi-1012 and Silakhor earthquakes resulted in a reduction in persistent displacement which could be contributed to a low earthquake maximum period. The maximum displacement of the structure was increased when the SMAs percent increased. Results demonstrated that the optimum SMAs value for braces was 20%, which minimized persistent displacement of the structure.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The Faculty of Civil Engineering, Semnan University, supported this work and the authors would like to acknowledge the academic staff of the Department of Earthquake Engineering for their full support.


