An Appraisal of Compressive Strength of Concrete Incorporated with Chemically Different Fly Ashes

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

An Appraisal of Compressive Strength of Concrete Incorporated with Chemically Different Fly Ashes

Atsushi Suzuki1 , * Open Modal Dinil Pushpalal2 Hiroo Kashima3
Authors Info & Affiliations
The Open Civil Engineering Journal • 14 Sep 2020 • RESEARCH ARTICLE • DOI: 10.2174/1874149502014010188

Abstract

Introduction:

Generally, the compressive strength of fly ash concrete differs depending on the properties of fly ash. This strength difference causes difficulties for concrete engineers to guarantee the strength of supplied concrete.

Methods:

This research firstly carried out the compressive strength tests on the concrete incorporated with fly ash possessing various chemical composition, which are high and low calcium fly ashes. The linear and nonlinear regression analyses were adopted to build the strength prediction model.

Results:

The chemical and physical properties of procured fly ash with high and low calcium contents have been quantified. Specifically, the compressive strength of concrete with high calcium fly ash demonstrates a strong correlation with calcium content, rather than physical properties such as the surface area and loss of ignition. Therefore, the compressive strength on 28th day can be assessed by a simple formula, taking CaO content of fly ash as an independent variable. In further, the strength on an arbitrary day can be predicted based on the 28th day strength and the replacement rate of fly ash.

Conclusion:

The two-step framework proposed in this research enables concrete engineers to evaluate the compressive strength of fly ash concrete with an error rate of less than 30%, within the applicable range addressed in this research.

Keywords: High calcium fly ash, Compressive strength, Prediction model, Chemical composition, CaO, Coal.

1. INTRODUCTION

Coal is a cheaper and easy fossil fuel for electricity production, which originates a huge amount of fly ashes as a byproduct. Currently, fly ash is mainly adopted in the construction industry by incorporating with concrete. Furthermore, the guidelines of using fly ash concrete have been published by prestigious institutions [1-3]. With increasing demand for coal for power generation, the promotion of fly ash concrete is inevitably required to prevent the negative environmental and social impact caused by the byproduct.

The compressive strength of fly ash concrete predominantly depends on the independent variables of a mixture, particularly the water-cement ratio and fly ash replacement rate. However, the strength of fly ash concrete varies depending on the quality of fly ash [4]. Generally, the chemical and physical properties of fly ash differ with the source of coal, production time, and the burning method of coal in power plants. Therefore, a strength prediction model is essential for the appropriate use of fly ash in concrete.

The fundamental concept of strength prediction was introduced by Saul [5] in 1951. Saul [5] quantified the prediction formula of compressive strength as the product of curing temperature and curing age. The formula is given in Eq. (1).

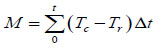(1)

Where M is the maturity at age t [°C day], Tc is the average temperature of concrete during the time interval [°C], Tr is the datum temperature [°C], t is an age, and Δt is the time interval [day].

However, it is widely recognized that Saul’s model underestimates the early age strength and overestimates the strength in later age [6].

Hansen and Pedersen [7] had proposed the concept of “equivalent age” given in Eq. (2). In Eq. (2), the nonlinear strength development was established by involving the exponential function.

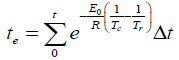(2)

Where te is the equivalent age at the reference curing temperature [day], E0 is the apparent activation energy [J/mol], and R is the gas constant (= 8.31 J/K mol).

In further, the apparent activation energy is predictable in Eqs. (3) and (4) [7].

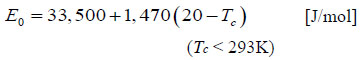(3)
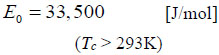(4)

However, the formula does not reflect the difference between cement and fly ash properties. Thereby, further investigation is necessary to generalize the prediction formula.

American Concrete Institute (ACI) [8] had proposed Eq. (5) for the strength prediction.

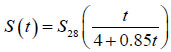(5)

Where S(t) is the compressive strength at age t [N/mm2] and S28 is the compressive strength on the 28th day[N/mm2].

However, ACI Committee 209 model [8] cannot estimate the compressive strength on 28th day. In addition, the above model does not consider the influence of the fly ash replacement rate, which is one of the most important determinants of fly ash concrete.

International Federation for Structural Concrete (CEB-FIP) [9] had also formulated Eq. (6).

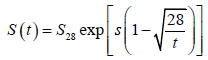(6)

Where s is constant, obtained from the experiment. CEB-FIP defines the value of s as 0.31 for the ordinary Portland cement [9].

Hedegaard and Hansen [10] have shown that Eq. (7) can be applied to fly ash concretes with high confidence, proving the reliability of the equation, using 660 sets of data. In the experimental series, there were three kinds of cement and two kinds of fly ash. The applicable scope range covers the c/w of 0.2 to 2.6 and the f/w of 0.0 to 2.0. Eq. (7) is reliable and easy to use, because of ready availability of the independent physical parameters such as cement content of concrete, c, fly ash content of concrete, f, and free water content of concrete, w, for a given mix proportion.

However, the values of three constants A, B, and E, have been trusted to individual concrete engineers to determine more accurate values for local materials and curing conditions, on the basis of results of trial mixes carried out on site.

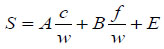(7)

where c is the cement content [kg/m3], f is the fly ash content [kg/m3], w is the water content [kg/m3], and A, B, E are arbitrary constants.

However, the relationship between arbitrary constants and chemical/physical properties of fly ash had not been defined by Hedegaard and Hansen [10]. Moreover, early age strength, such as compressive strength at 3rd day, was not investigated due to the lack of experimental data.

Yildirim et al., addressed the discrepancy of compressive strength of fly ash concrete by modifying the Hedegaard’s model [11]. Yildirim’s model is given in Eq. (8). Yildirim et al. [11], introduced an efficiency factor, k, which varies depending on the types of fly ash, especially regarding Class C and Class F.

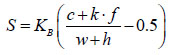(8)

Where h is the air content in concrete [m3/m3], k is the efficiency factor [-], KB is the Bolomey coefficient [-].

However, efficiency factor k was not defined as a function of chemical or physical properties of fly ash, limiting the usage as a prediction model.

Han et al. [12], proposed a prediction model as given in Eq. (9).


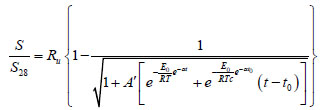(9)

Where Ru is the ultimate relative strength [-], t0 is the age when the strength development is assumed to begin [day], α is arbitrary constant [-], and A’ is constant [-]. However, t0 can be estimated as 0 day, and A’ is not a function of age and mixture proportion, but a constant equal to 107 [12]. Again, there are three undefined parameters (Ru, E0 , and α) in this model, and no methodology has been proposed to calculate 28th day compressive strength, i.e., 28th day strength should still be measured through laboratory tests.

Besides the above mentioned decades-old pioneering studies on strength prediction models, there are many recent studies on this issue [13-28]. They addressed a wide range of mix proportions, various types of cement and fly ashes, curing conditions, etc.

As a representative example, Rohman et al., investigated the fly ash concrete combined with the recycled aggregate [25]. The compressive strength of concrete with various water-cement ratio and the recycled coarse aggregate ratio was studied to build more environmentally-friendly fly ash concrete. Additionally, the prediction model of compressive strength was proposed by the multiple regression analyses using the recycled coarse aggregate ratio, fly ash replacement ratio, and water-cement ratio as the variables.

Another research conducted by Tipraj et al., carried out a series of compressive and flexural strength tests on the fly ash concrete with the fly ash replacement of up to 60% [28]. In further, the chemical activation was attempted to broaden the applicability of fly ash concrete.

However, it is still a great challenge to build a prediction equation; because only a few studies have attempted to address the issue in a statistical manner.

The aforementioned discussion corroborates that a simple prediction model representing the chemical properties of fly ash as a continuous function does not exist, while it is essential to increase the use of fly ash in concrete. In addition, the formula should be simple enough for the practical use among concrete engineers working in factory environments, where the sophisticated software or equipment may not be available.

Accordingly, at the beginning, this research carries out the compressive strength test on the concrete specimens incorporated with fly ash possessing different chemical compositions. This research firstly establishes a prediction model, in which the 28th day compressive strength can be estimated using independent parameters of a given mix proportion, without using any arbitrary or intangible constants. Secondly, an estimation method for predicting compressive strength on a random day is proposed. The main purpose of this research is to build a simple prediction model by extracting the most influential components for strength. The predictability of the 28th day strength, the possibility of calculating the strength at any age, and the simplicity of the proposed model are the significances of this research. Ultimately, the outcome of this research realizes the safer use of fly ash concrete, promotion of fly ash concrete, reduction of environmental impact caused by a byproduct, and mitigation of burden of concrete engineers.

2. MATERIALS AND METHODS

2.1. Materials

2.1.1. Fly Ash

Four types of high calcium fly ash (hereinafter referred to as MNG1, MNG2, MNG3, and MNG4) were collected from Ulaanbaatar City 4th coal power plant by the authors. A low calcium fly ash with totally different chemical properties from above collected from a Japanese power plant (hereinafter referred to as JPN) was included in this experimental series.

Mongolia has a very high share of electricity production from coal sources, which accounted for 93% of total electricity production. Additionally, the fly ash in Mongolia generally contains a large amount of calcium according to the preliminary survey by the authors. In contrast, the fly ash from the Japanese power plant possesses comparatively low CaO, which is less than 10%. The locations of procurement were determined for covering a broad range of fly ash properties.

In Table 1, the chemical composition, specific gravity, surface area, and loss of ignition of each fly ash are tabulated. All Mongolian fly ashes have over 10% of CaO in contrast to the Japanese one, whose CaO amount is only 5.0%. The chemical composition of the fly ash was measured by an X-ray fluorescence spectrometer. The specific gravity was measured in conformity to JIS A 6201 [29]. The surface areas were calculated from the result of mean diameter gauged by the laser diffraction and scattering method analyzer. In Table 1, the chemical properties differ from one ash to another. This research refers this difference as “chemically different fly ashes.”

2.1.2. Cement

Class 42.5 Portland cement (specific gravity: 3.00) available in the market was used. The chemical composition is given in Table 2.

2.1.3. Sand, Gravel, Superplasticizer

The sand was sieved through 5 mm mesh. The gravel was 20 mm in maximum size. The polycarboxylate ether-based high range water reducing admixture was used to achieve the appropriate slump for the concrete mixtures.

2.2. Mix Proportions

Tables 3 and 4 show the mix proportions of MNG1 and MNG2 cases and MNG3, MNG 4 and JPN cases. In this research, not only the influences of the chemical property of fly ash but also influences of fly ash replacement rate on compressive strength were considered. The maximum fly ash replacement rate was 40%. Two water binder ratios appropriate to each fly ash were adopted. The amount of superplasticizer was adjusted in each mix proportion to keep the workability equal in all mix proportions, at a slump of 200±20 mm, thereby obtaining equally compacted specimens.

Table 1.
Properties of fly ash.
Type of Fly Ash Chemical Composition (wt. %) Specific
Gravity
[-]		 Surface Area
[cm2/cm3]		 Loss of Ignition
[%]
SiO2 Al2O3 Fe2O3 CaO SO3 MgO Others
MNG1 43.4 12.4 7.1 23.8 4.2 4.6 4.5 2.46 15409 0.80
MNG2 47.2 14.2 12.0 18.6 1.2 2.2 4.6 2.49 26096 1.45
MNG3 47.5 13.0 10.8 17.4 2.3 2.8 6.2 2.38 22298 0.80
MNG4 49.4 13.0 11.0 16.4 1.6 1.9 6.7 2.36 20242 0.50
JPN 46.3 29.2 7.1 5.0 0.5 0.8 11.1 2.26 15158 5.70
Table 2.
Chemical composition of Portland cement (wt. %).
SiO2 Al2O3 Fe2O3 CaO SO3 Residue Insoluble Loss of Ignition Others Total
16.5 7.6 2.3 54.3 3.0 9.1 4.4 2.8 100

2.3. Specimen, Curing Condition, and Strength Test

One axis horizontal mixer was used to mix concrete. The size of the molds was ϕ100×200 mm. The specimens were demolded after two days from the casting and cured in water at 20±2°C. The compressive strength tests were conducted on the 3rd, 7th, 28th and 91st days. The compressive strength tests were carried out in confirmatory with JIS A 1108 (Method of test for compressive strength of concrete) [30]. The testing apparatus is exhibited in Fig. (1).

Table 3.
Mix proportions of MNG1 and MNG2 cases.
W/B
[%]		 FA/(C+FA)
[%]		 Unit Weight [kg/m3]
W C S G FA Ad
46 0 165.1 358.2 1006.9 884.9 0 5.0
10 320.1 35.6 5.0
20 282.5 70.6 4.9
30 245.4 105.2 4.9
40 208.8 139.2 4.9

Table 4.
Mix proportions of MNG3, MNG4, and JPN cases.
W/B
[%]		 FA/(C+FA)
[%]		 Unit Weight [kg/m3]
W C S G FA Ad
44 0 157.7 361.4 1015.9 892.8 0 6.5
10 322.5 35.8 5.0
20 284.6 71.1 5.0
30 247.2 105.9 4.9
40 210.4 140.2 4.9

Fig. (1). Specimens and the testing apparatus: (a) specimen; (b) compression testing machine.
Fig. (2). Compressive strength development: (a) MNG1; (b) MNG2; (c) MNG3; (d) MNG4; (e) JPN.

3. RESULTS

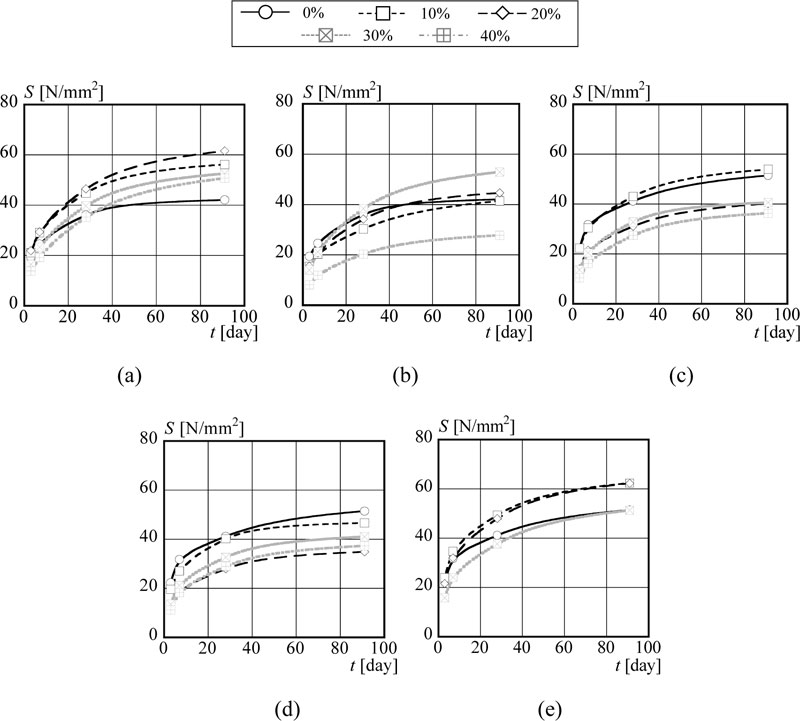
Fig. (2) illustrates the difference in compressive strength by the fly ash replacement rate. In Fig. (2), concrete incorporated with MNG1 shows a distinctive compressive strength than others. In the case of 10% and 20% replacement rates, the compressive strength exceeds that of concrete without fly ash even as early as on the 3rd day. Finally, all mix proportions incorporated with fly ash MNG1 surpassed the concrete without fly ash from the 28th day. In contrast to that, the compressive strengths of concrete incorporated with MNG2, MNG3, MNG4 and JPN are relatively low. MNG2 and JPN cases show the typical strength enhancements due to the pozzolanic reaction of fly ash in old ages. However, the high replacement rates such as 40% can give only about 70% of compressive strength of concrete without fly ash even on the 91st day. It can be assumed that this is predominantly due to the chemical composition of fly ash.

Supporting the above assumption, Papadakis studied high calcium fly ash as an additive in a mortar and concluded that the final strength gain of the mortar is roughly proportional to the content of calcium bearing mineral phases in a given mortar volume [31]. A considerable number of publications regarding the effect of fly ashes on concrete, especially of low-calcium fly ash, have discussed the strong relationship of particle size and ignition loss with compressive strength. Hwang et al., reported that the strength development originates more actively in fly ash with larger surface area [32]. However, MNG1, whose surface area is the smallest among the Mongolian fly ash demonstrates the highest compressive strength. Additionally, the loss of ignition also does not show a significant relationship. This is inferred that calcium-bearing mineral phases of high calcium fly ash work as a reactive additive than an inert filler, giving a higher early strength comparable to control concrete that is unlikely to happen when the low calcium fly ash is used.

Fig. (3). Comparison between experimental and predicted value.
Table 5.
Regression coefficients.
Type of fly ash A B E
MNG1 31.7 10.3 -14.9
MNG2 41.4 21.5 -45.2
MNG3 38.0 12.4 -37.6
MNG4 39.3 14.1 -41.2
JPN 63.0 40.1 -88.0



4. DISCUSSION

4.1. Prediction Model of Compressive Strength on the 28th Day

This research attempts to construct a prediction model of compressive strength on the 28th day based on Hedegaard’s model shown in Eq. (7), by defining three arbitrary constants A, B, and E.

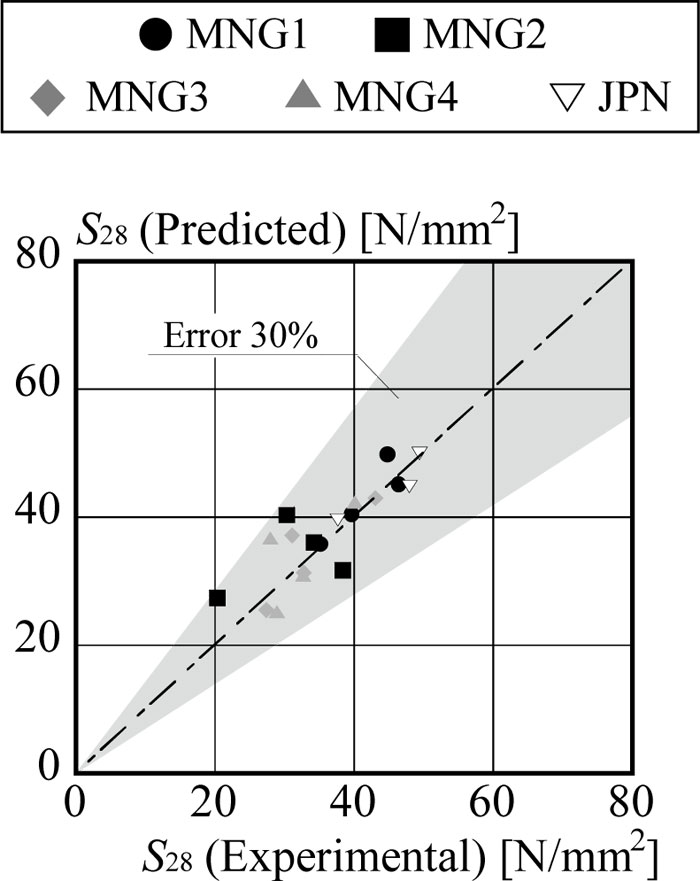
Multiple regression analysis was conducted for estimating the relationship between 28th day compressive strength as a dependent variable and both c/w and f/w as predictors. The obtained constants are tabulated in Table 5. The comparison between experimental results and predicted results from obtained constants is illustrated in Fig. (3) The experimental results are predicted with an error rate of less than 30%. It is assumed that the discrepancy among obtained constants was originated by the difference in fly ash properties. Therefore, this research attempts to assess them based on the fly ash properties.

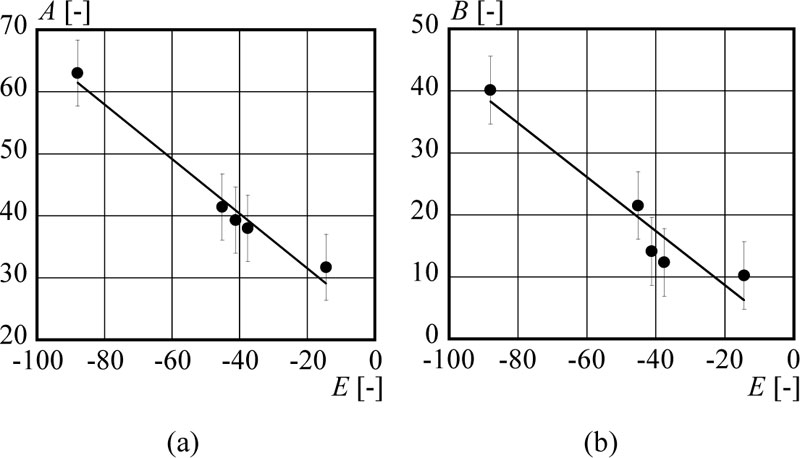
Figs. (4a & b) show the relationship between A and E, and B and E. The regression coefficients are -0.99 and -0.95, respectively, which corroborate the strong linear relation with the constant E. By carrying out single regression analysis, the following formulae to calculate constant A and B are obtained.

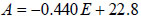(10)
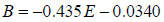(11)

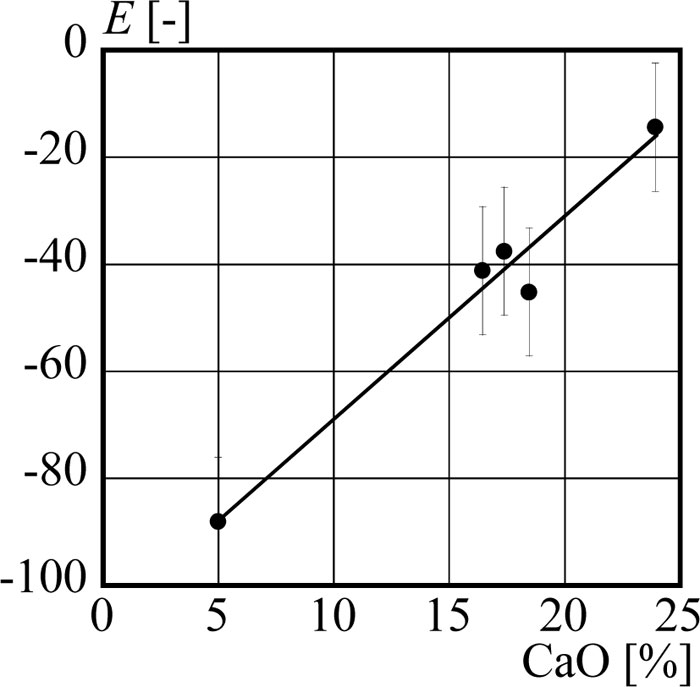
Therefore, a desired prediction model can be constructed by quantifying constant E, because other constants can be obtained from constant E. Table 6 tabulates the correlation coefficients between constant E and elements, expressed as oxides in the fly ash. In Table 6, CaO indicates the highest correlation coefficient. Therefore, constant E can statistically be represented precisely by the CaO content alone, which realizes a simple prediction equation of the compressive strength.

Based on the correlation investigation above, the authors suggest to evaluate constant E using CaO content in fly ash as a determinant, which possesses a strong relationship with constant E as demonstrated in Fig. (5). Furthermore, it is widely acknowledged that the CaO-bearing mineral phases strongly influence the compressive strength of concrete [33-35] as well as the identical characteristics observed in the previous section. Therefore, the CaO content is inferred to be appropriate as an independent variable. The obtained formula to assess the constant E is given below.

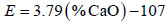(12)

where (%CaO) denotes the percent CaO content.

Fig. (4). Relationship between obtained constants: (a) E and A; (b) E and B.
Table 6.
Correlation coefficient between constant E and elements expressed as oxides.
Element oxides Correlation coefficient
SiO2 -0.29
Al2O3 -0.92
Fe2O3 0.17
CaO 0.98
SO3 0.89
MgO 0.91
Fig. (5). Relationship between constant E and CaO content.
Fig. (6). Comparison between experimental and predicted value (28th day strength).

Finally, the prediction model for the 28th day strength of fly ash concrete can be presented as follows. Here, constant E is designated as “chemical factor, Cf.”

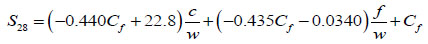(13)

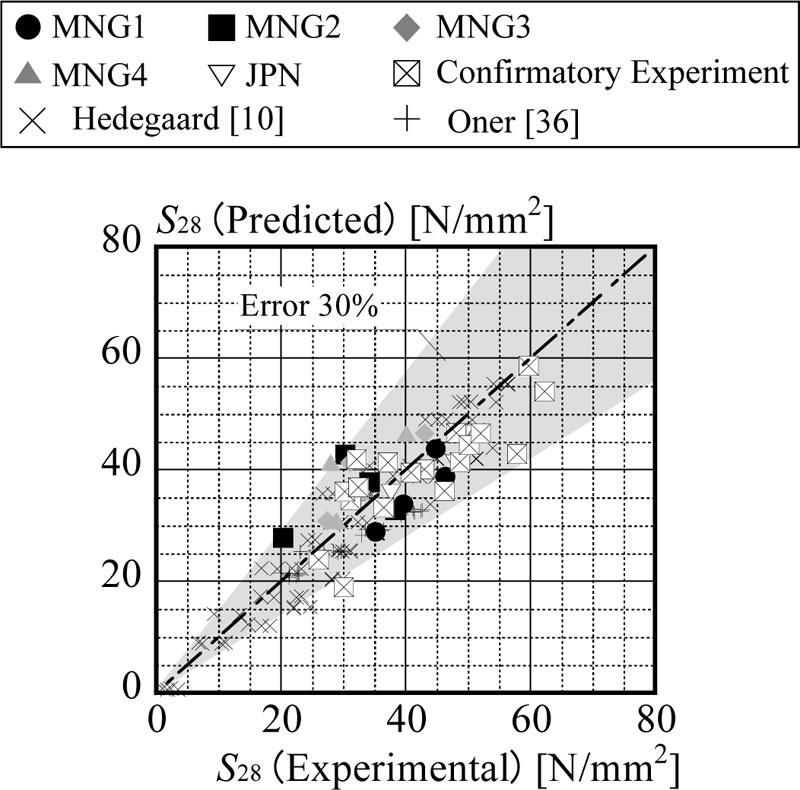
Fig. (6) shows the comparison between experimental results and predicted results by Eq. (13). In addition, the results of confirmatory experiment, Hedegaard’s experiment [10], Oner’s experiment [36] were utilized to prove the validity of the model. Fig. (6) proves that the proposed prediction model can predict the experimental results with the error rate of less than 30%.

4.2. Prediction Model of Compressive Strength on an Arbitrary Day

Based on the findings above, this research further generalizes the prediction model for the compressive strength on an arbitrary day referring Han’s equation shown in Eq. (9) [12].

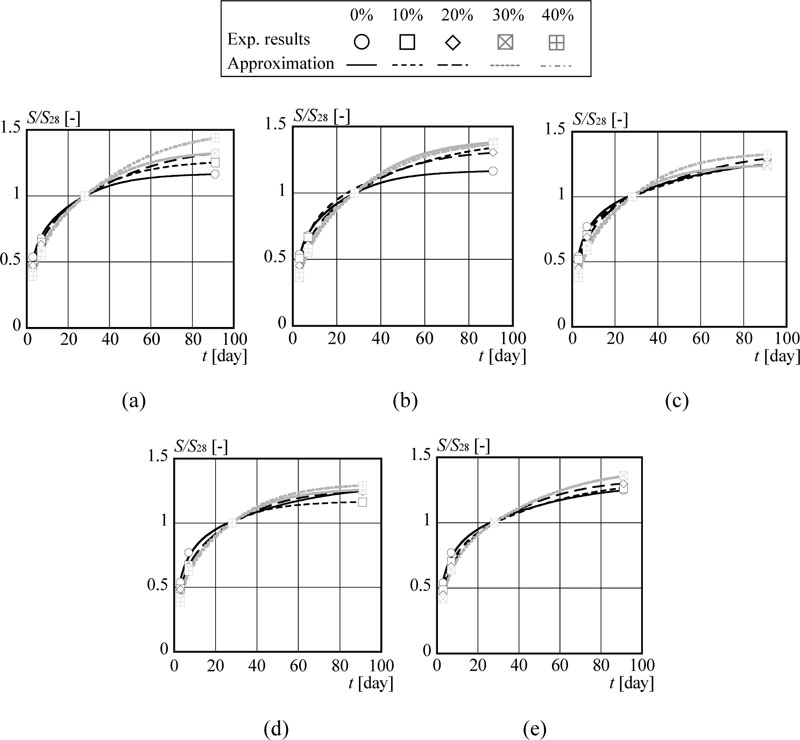
Figs. (7a-e) show the relative strength development (S/S28). Additionally, the result of approximation by Eq. (9) is illustrated in Fig. (7) as well. From Fig. (7), it can be confirmed that the approximation line obtained from Eq. (9) based on the least squares method precisely predicts the relative strength development. In all cases, Eq. (9) shows high R2, over 0.99.

The relative compressive strength becomes lower with higher fly ash replacement rate at early ages. This is because the amount of cement, which contributes to strength development in early ages, is low in the mixture. In contrast, the relative strength becomes higher with higher fly ash replacement rate in later ages. It can be assumed that the pozzolanic reaction occurs more actively in high fly ash replacement rate cases compared with low fly ash replacement rate cases.

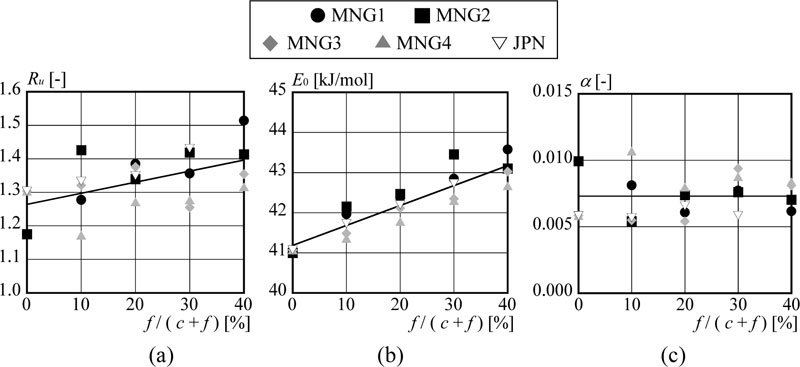
The relationships between obtained constants from Eq. (9) and fly ash replacement rate are displayed in Fig. (8). Fig. (8a) shows that Ru has a positive relationship with fly ash replacement rate. This is due to the pozzolanic reaction as stated above. The apparent activation energy E0 becomes larger with an increase in the fly ash replacement rate similar to Ru. The concept of apparent activation energy has been previously applied to cementitious systems by Barnett et al. [37], and Bentz [38]. The apparent activation energy is generally derived as a slope of the Arrhenius plot based on the inverse of absolute temperature and natural logarithm of rate constant. However, in this research, the apparent activation energy is directly calibrated based on the nonlinear least squares method. This confirms that the compressive strength is not developed well in higher fly ash replacement rates. However, α does not show the clear relationship with the fly ash replacement rate.

Therefore, the evaluation formulae to assess Ru and E0 can be presented as functions of fly ash replacement rate as given in Eq. (14) and Eq. (15). α is assessed by Eq. (16) by calculating the average of all cases.

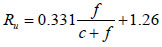(14)
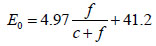(15)
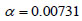(16)
Fig. (7). Relative strength development: (a) MNG1; (b) MNG2; (c) MNG3; (d) MNG4; (e) JPN.
Fig. (8). Relationship between obtained constants and fly ash replacement rate: (a) Ru; (b) E0; (c) α.
Fig. (9). Calculation flow of compressive strength on an arbitrary day.

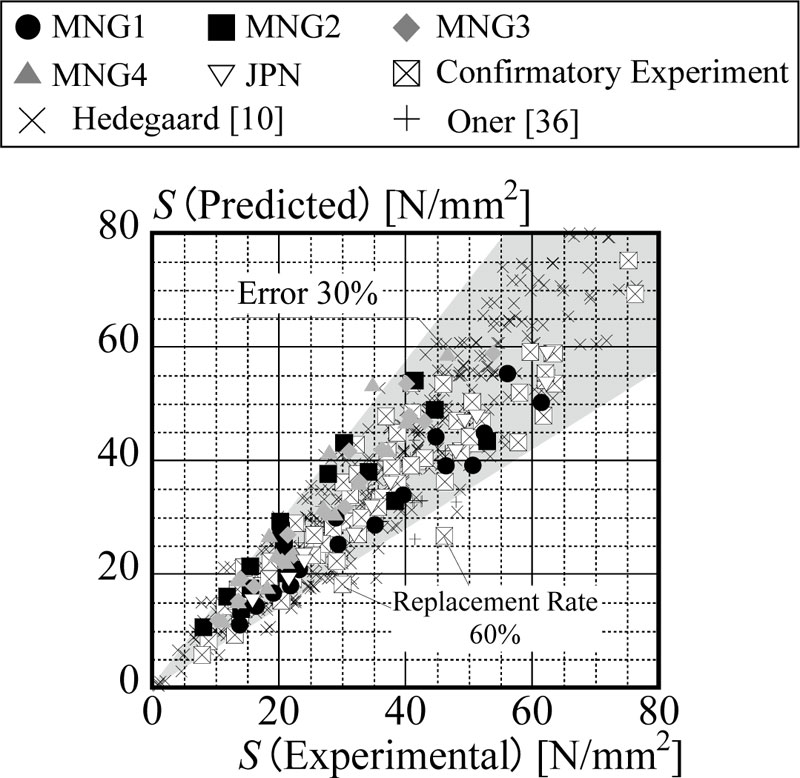
Based on the discussion above, the compressive strengths on an arbitrary day can be predicted using Eqs. (9), (12), (13), (14), (15), and (16) as illustrated in Fig. (9). The comparison between experimental results and predicted results is illustrated in Fig. (10). As same as Fig. (6), the results of confirmatory experiment, Hedegaard’s experiment [10], and Oner’s experiment [36] were adopted to prove the validity of proposed equations. The proposed prediction model can assess most of the experimental results with the error rate of less than 30%.

It should be noted that the applicable scope range of the proposed equation covers 5.0 to 23.8% in CaO content. Also, this research has addressed only one type of cement with the chemical and physical properties given in Table 2.

Fig. (10). Comparison between experimental and predicted results (an arbitrary day strength).

CONCLUSION

This research has taken a statistical approach to build a simple prediction model of compressive strength of concrete incorporated with fly ash with different properties. The remarkable findings are summarized below:

(1) The compressive strength of fly ash concrete varies with the properties of fly ash. Especially, a large discrepancy has been confirmed in early-age-strength.

(2) The compressive strength of concrete with high calcium fly ash demonstrates a strong correlation with calcium content, rather than physical properties such as the surface area and loss of ignition.

(13) A simple prediction model for estimating the 28th day compressive strength has been established by taking water, cement, and fly ash content in the mixture; and the calcium oxide content of the fly ash as independent parameters.

(4) The compressive strength on an arbitrary day can be predicted, when incorporating fly ash containing 5.0 to 23.8% of CaO, using calculated compressive strength on the 28th day and fly ash replacement rate.

The authors believe the two-step framework proposed in this research will be an example for future researchers to work on prediction models. The influence of cement properties will be investigated experimentally and analytically in our future research. Influential cement properties will be included to improve the prediction model proposed in this paper. It is understood that a simplified quantifying method of CaO content is desirable, particularly for rough factory environments where the sophisticated instruments cannot be installed. This issue will also be addressed in future research.

CONSENT FOR PUBLICATION

Not applicable.

AVAILABILITY OF DATA AND MATERIALS

The data supporting the findings of the article is available in the [Tohoku University Repository] at [http://hdl.handle.net/10097/63771], reference number [10097/63771].

FUNDING

Part of this work was funded by JSPS KAKENHI. Grant Number: JP 25303004.

CONFLICT OF INTEREST

The authors declare no conflicts of interest, financial or otherwise.

ACKNOWLEDGEMENTS

The experiments were supported by Mr. Ochirbat Batmunkh and the staff in Premium Industrial & Engineering LLC (Mongolia). Our deepest gratitude goes to their sincere support. We would like to thank eight anonymous reviewers for their comments and helpful suggestions on the first draft of this paper.

REFERENCES

1 Use of Fly Ash Concrete, ACI Committee 232, . 2 Recommendations for practice of concrete with fly ash, Architectural Institute of Japan, . 3 EN 450-1: 2012 Fly Ash for Concrete, Definition, specifications and conformity criteria, European Committee for Standardization, . 4 S. Honda, and Y. Shiiba, Effect of several types of fly ashes on properties of concrete, Proceedings of Japan Concrete Institute, Japan Concrete Institute, pp. 351-356. 5 A.G.A. Saul, "Principles underlying the steam curing of concrete at atmospheric pressure", Mag. Concr. Res., vol. 2, pp. 127-140.[CrossRef Link] 6 N.J. Carino, and R.C. Tank, "Maturity functions for concrete made with various cements and admixtures", ACI Mater. J., vol. 89, no. 2, pp. 188-196. 7 P.F. Hansen, and E.J. Pedersen, "Maturity computer for controlled curing and hardening of concrete", Nordisk Betong, vol. 1, pp. 21-25. 8 Prediction of creep, shrinkage and temperature effects in concrete structures, ACI Committee 209, . 9 CEB-FIP Model Code 1990, vol. 37, Thomas Telford Services Ltd., . 10 S.E. Hedegaard, and T.C. Hansen, "Modified water/cement ratio law for compressive strength of fly ash concretes", Mater. Struct., vol. 25, no. 149, pp. 273-283.[CrossRef Link] 11 H. Yildirim, M. Sümer, V. Akyüncü, and E. Gürbüz, "Comparison on efficiency factors of F and C types of fly ashes", Constr. Build. Mater., vol. 25, no. 6, pp. 2939-2947.[CrossRef Link] 12 S-H. Han, J-K. Kim, and Y-D. Park, "Prediction of compressive strength of fly ash concrete by new apparent activation energy function", Cement Concr. Res., vol. 33, no. 7, pp. 965-971.[CrossRef Link] 13 S. Tangtermsirikul, T. Kaewkhluab, and P. Jitvutikrai, "A compressive strength model for roller-compacted concrete with fly ash", Mag. Concr. Res., vol. 56, no. 1, pp. 35-44.[CrossRef Link] 14 H. Quan, and H. Kasami, "Experimental study on effects of type and replacement ratio of fly ash on strength and durability of concrete", Open Civ. Eng. J., vol. 7, pp. 93-100.[CrossRef Link] 15 K.V. Ramesh, M.D. Raju, and K. Rekha, "A Study on high volume fly ash concrete exposed to elevated temperatures", Americ. Jour. Of Eng. Res., vol. 5, no. 11, pp. 227-238. 16 S. Dey, "Study of compressive strength of high volume fly ash concrete with varying proportion of fly ash and silica fume", SSRG Int’l Jour. Of Civil Eng., vol. 3, no. 3, pp. 3-6.[CrossRef Link] 17 K.L. Lin, T.W. Cheng, C.H. Ho, Y.M. Chang, and K.W. Lo, "Utilization of circulating fluidized bed fly ash pozzolanic material", Open Civ. Eng. J., vol. 11, pp. 176-186.[CrossRef Link] 18 L. Wang, K. Uji, and A. Ueno, "Evaluation on reaction efficiency coefficient of fly ash based on threshold value of effective replacement ratio", Cem. Sci. & Concr. Tech., vol. 71, pp. 645-652.[CrossRef Link] 19 M. Solikin, and B. Setiawan, "The effects of design strength, fly ash content and curing method on compressive strength of high volume fly ash concrete: A design of experimental", MATEC Web of Conferences, vol. 103, p. 01003.[CrossRef Link] 20 V. Manohar, and P.P. Raju, "Comparative study on compressive strength of fly ash concrete", Int’l Jour. of Civil Eng. & Tech., vol. 8, no. 4, pp. 1668-1676. 21 M. Abushad, and M.D. Sabri, "Comparative study of compressive strength of concrete with fly ash replacement by cement", Int’l Res. Jour. of Eng. & Tech., vol. 4, no. 7, pp. 2627-2630. 22 J. Mahesh, K. Nagamony, and G. Chettyar, "Compressive strength analysis of fly ash concrete with fine aggregate of river sand and manufactured sand", Int. J. Pure Appl. Math., vol. 117, no. 9, pp. 107-111. 23 K.V. Sabarish, R.V. Raman, R. Ancil, R.W. Raja, and P.S. Surendar, "Experimental studies on partial replacement of cement with fly ash in concrete elements", Int’l Jour. of Civil Eng. & Tech., vol. 8, no. 9, pp. 293-298. 24 A. Wardhono, "Comparison study of class F and class C fly ashes as cement replacement material on strength development of non-cement mortar, The 2nd Annual App", Sci. & Eng. Conf., vol. 288, .012019 25 R.K. Rohman, and S. Aji, "Effect of fly ash on compressive strength of concrete containing recycled coarse aggregate", AIP Conf. Proc., vol. 2014, .020097[CrossRef Link] 26 K.V. Madurwar, A.N. Burile, and A.M. Sorte, "Compressive strength of cement & fly ash mortar: A case study", Proc. Of Sust. Infr. Devel. & Manag., vol. 2019, .3376014[CrossRef Link] 27 H.J. Chen, N.H. Shih, C.H. Wu, and S.K. Lin, "Effects of the loss on ignition of fly ash on the properties of high-volume fly ash concrete", Sustainability, vol. 11, no. 9, p. 2704.[CrossRef Link] 28 B. Tipraj, M.G. Prasad, E.L. Prasanna, A. Priyanka, and P.K. Hugar, "Strength characteristics of concrete with partial replacement of cement by fly ash and activated fly ash", Int’l Jour. of Recent Tech. & Eng., vol. 8, no. 4, pp. 4299-4305.[CrossRef Link] 29 Fly Ash for Use in Concrete, JIS A 6201, . 30 Method of test for compressive strength of concrete, JIS A 1108, . 31 V.G. Papadakis, "Effect of fly ash on Portland cement systems Part II. High-calcium fly ash", Cement Concr. Res., vol. 30, pp. 1647-1654.[CrossRef Link] 32 K. Hwang, T. Noguchi, and F. Tomosawa, "Prediction model of compressive strength development of fly-ash concrete", Cement Concr. Res., vol. 34, pp. 2269-2276.[CrossRef Link] 33 Y. Zhang, W. Sun, and L. Shang, "Mechanical properties of high performance concrete made with high calcium sulfate fly ash", Cement Concr. Res., vol. 27, no. 7, pp. 1093-1098.[CrossRef Link] 34 C.S. Poon, S.C. Kou, L. Lam, and Z.S. Lin, "Activation of fly ash / cement systems using calcium sulfate anhydrite (CaSO4)", Cement Concr. Res., vol. 31, no. 6, pp. 873-881.[CrossRef Link] 35 Y. Shen, J. Qian, and Z. Zhang, "Investigations of anhydrite in CFBC fly ash as cement retarders", Constr. Build. Mater., vol. 40, pp. 672-678.[CrossRef Link] 36 A. Oner, S. Akyuz, and R. Yildiz, "An experimental study on strength development of concrete containing fly ash and optimum usage of fly ash in concrete", Cement Concr. Res., vol. 35, pp. 1165-1171.[CrossRef Link] 37 S.J. Barnett, M.N. Soutsos, S.G. Millard, and J.H. Bungey, "Strength development of mortars containing ground granulated blast-furnace slag: Effect of curing temperature and determination of apparent activation energies", Cement Concr. Res., vol. 36, pp. 434-440.[CrossRef Link] 38 D.P. Bentz, "Activation energies of high-volume fly ash ternary blends: Hydration and setting", Cement Concr. Res., vol. 53, pp. 214-223.[CrossRef Link]