Performance of Bridge Envelope During Earthquake Using Finite Element and Artificial Neural Network Techniques

2.1. Finite Element Modeling (FEM)

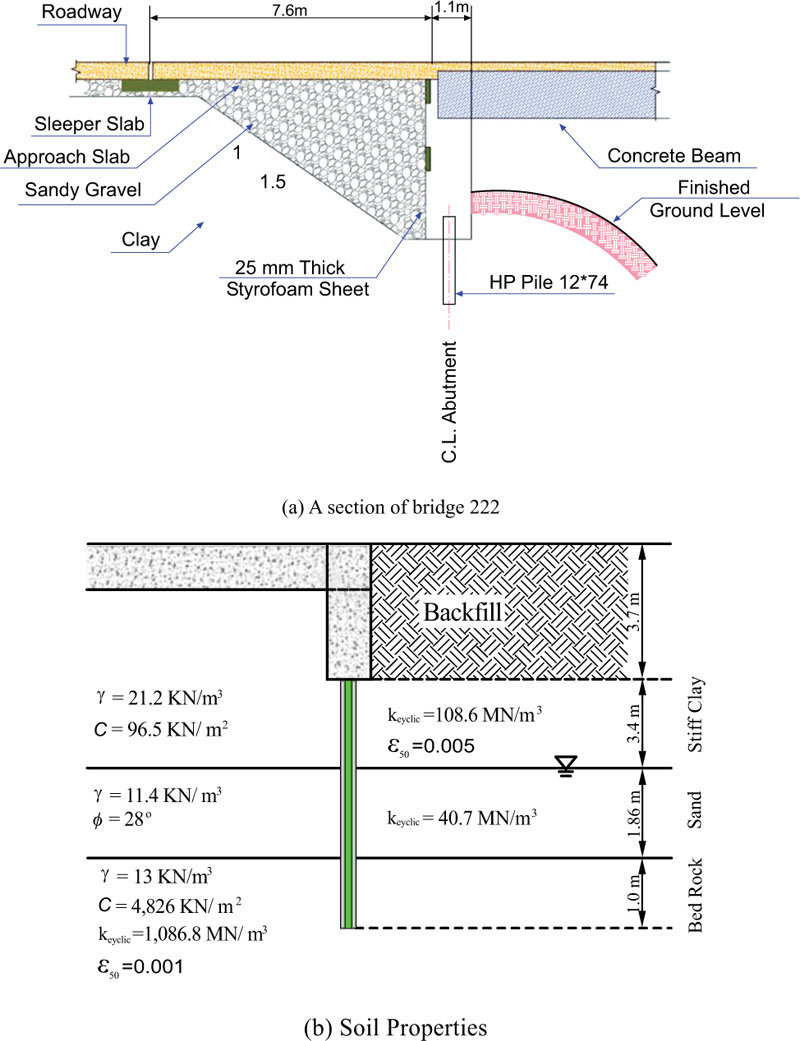
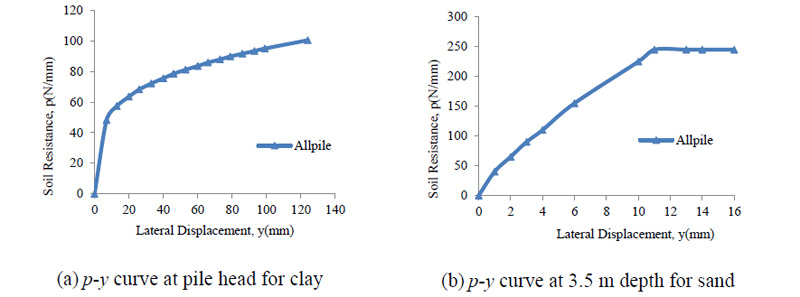
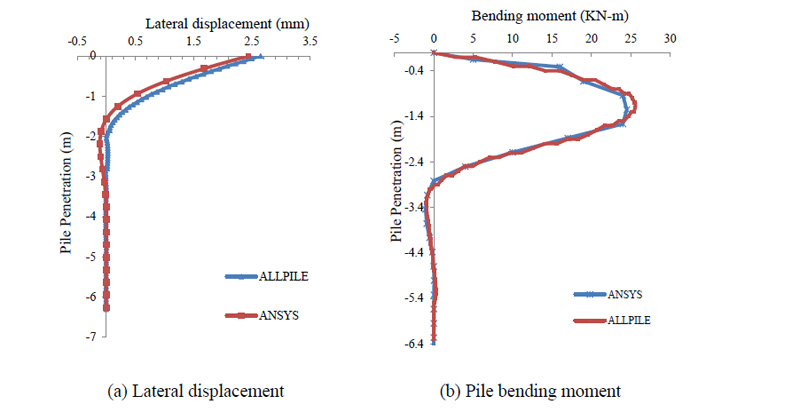
Soil pile and soil abutment interactions, known as soil structure interactions (SSIs), are related to geotechnical behavior, while abutment backwall and pile abutment connections are related to the yielding of structural connections. SSI generally has a more influential parameter than the yielding of structural connections, because soil exhibits nonlinear and hysteretic behavior even over a small range of deformations. In addition, the yielding of structural connections may never occur in a lifetime of bridge structures, if properly designed. The classical p-y curve technique is assumed to deliver a load-deformation curve of laterally loaded SSI behaviours. p-y curves are generated using the COM624P developed by Wang and Reese [36]. The p-y curve technique is one of the SSI examination methods based on the modulus of the subgrade reaction approach. The substitution of nonlinear p-y curve springs in the governing equation was done instead of using a traditional linear winkler spring. Lateral analysis in AllPile (AP) software utilizes the finite difference method for the modeling of SSI. In lateral loading, the pile shaft deflects and exerts pressure on the adjacent soils, resulting in the generating of lateral resistance (pressure) between soils and pile. By integrating lateral pressure, shear, moment, rotation and deflection, an analysis of the pile and soil interaction and behavior is obtained. Also, for validation of FE software (i.e., ANSYS) and AP software, one pile of implemented IAB is chosen and modelled with FE software by p-y curves taken from AP software; then the output of FE and AP is compared. Fig. (1a) shows bridge 222, Pennsylvania which is used in this research. Also, soil parameters were taken from Bridge 222 soil profile for clay above water table and sand, displayed in Fig. (1b). Samples of p-y curves generated by AP software are presented in Fig. (2). Both AP and FE softwares display highly similar responses to the lateral force on the pile head. Therefore, it may be concluded that it is possible to expect acceptable responses for SSI within the bridge piles. As shown in Fig. (3) maximum displacement was 2.44 mm by FE software and 2.65 mm by AP, while the maximum moment is 24.5 kN-m by FE and 25.6 kN-m by AP. FE software predictions of pile behavior are similar to AP with percentage differences of 8% and 8.5%, for maximum displacement and maximum moment respectively. Element length in the FE pile model is relatively coarse (33 mm) compared to the length used in AP (30 mm). Therefore, some small differences in moments at a depth of approximately 3 mm are expected to appear, where a short distance of two adjacent inflection points occurs.

Table 1 presents a summary of IAB structure in this research. The abutment is supported by a single row of weak axis-oriented steel piles by HP12×74. In FE, BEAM3 element was used to combine a composite slab and four girder sections. This beam member was subdivided into 10 pieces, all located on a composite elastic neutral axis. An elastic modulus of girders was used as a reference modulus, so that slab and parapet widths were transformed using corresponding modulus ratios. AASHTO LRFD [37] was used to determine a concrete modulus of elasticity based on a girder’s concrete strength of 55.2 MPa. Table 2 reviews the material properties of the superstructure.

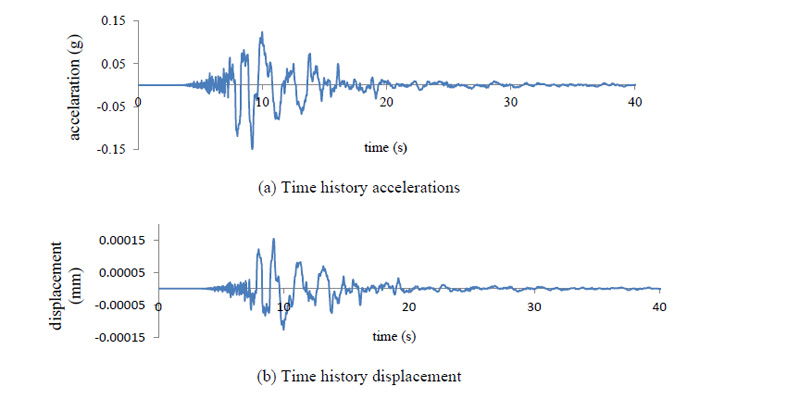
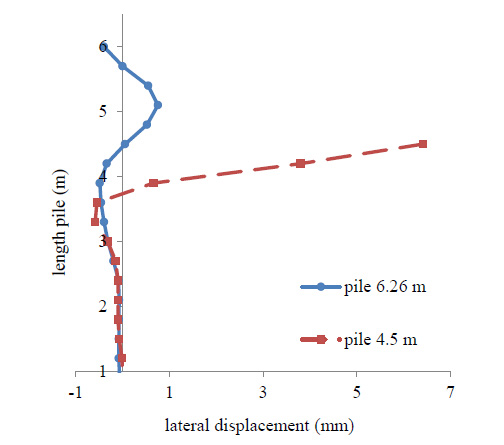
Fig. (4) shows time history accelerations and displacement at the height of 2m below the surface of the soil profile. When time history analysis is performed and convergent results are obtained, structure reaction at the selected time can be seen. The output which is investigated in this study includes lateral displacement on pile head, bending moment at pile head and axial force in girder. As shown in Fig. (5), the highest lateral deflection of the piles along the length is always at the interface of the pile abutment. The pile deflection at the top of pile with 6.26 m length is 0.397 mm and pile deflection at the top of pile with 4.5 m length is 6 mm. In time history analysis for each time, applied particular displacement on structures and behavior of the structure is checked at that time. The largest lateral displacements above and below the abutment walls during the time history analysis are presented in Table 3 for abutments, showing how generally the maximum wall lateral displacements are greater at the bottom and well matched with the pile deflection. Consequently, essentially all lateral and longitudinal loads applied to the superstructure of such bridges are transmitted directly to abutment embankments. It is obvious that the stiffness of the soil to the rear of the abutment and in the vicinity of the piles affects the pile deflection, which is reduced when the soil stiffness is reduced. The highest positive and negative moments in head of piles for the duration of the time history analysis are presented in Table 4. It appears that there is a normal reduction in the girder moments along the bridge, within the span due to stiffness of the soil at the back of the abutment and in the area surrounding the piles, like the pile deflection and abutment displacement.

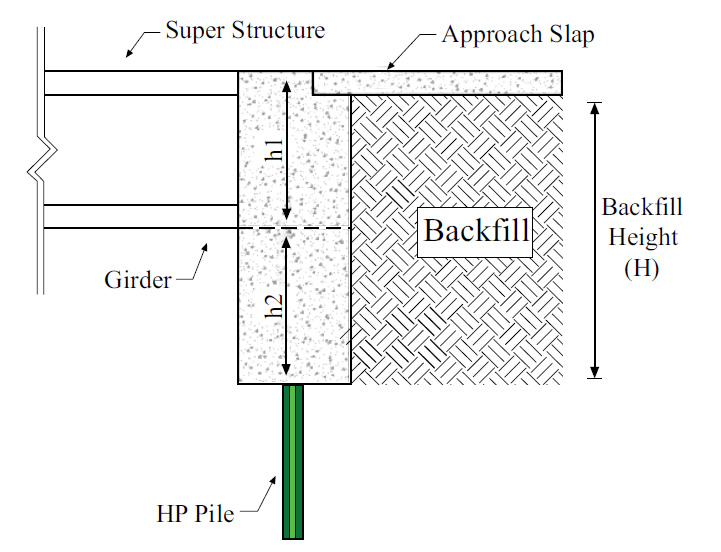
An adopted common IAB foundation configuration consists of a single row of steel HP piles supporting a cast in place and wall type abutment and backwall with MPa supporting girders. Bridge span (L) and height of backfill (H) are the two structural bridge dimensional parameters considered in the parametric analysis. To portray short to medium bridges, bridge spans were chosen. Backfill heights were chosen to reflect medium to high abutments of the stub type. The bridge spans considered were 18.3, 34.5, and 65.4 m. The overall backfill height from the bottom of the abutment pile cap to the bottom of the approach slab is expressed by H. For each IAB, the level of the roadway was retained, while the abutment below the height of the girder seat was shown in Fig. (6) for various bridge lengths. As a conclusion of this convention, the construction joint between abutment and backwall has different elevations as the bridge span changes.

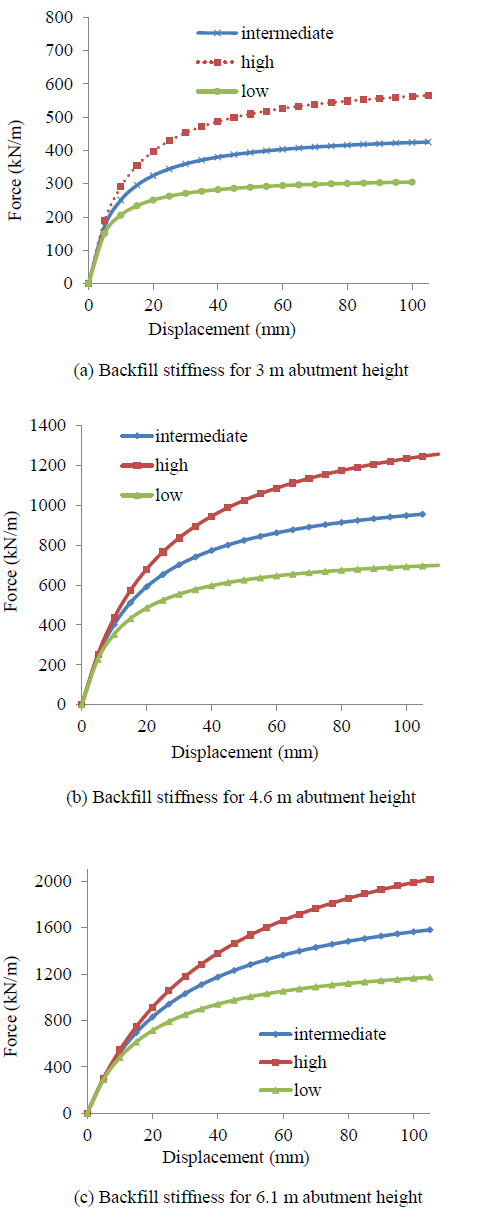
Backfills behind abutments, due to soil density, exert lateral loads during bridge contraction while backfills also exert resistances during bridge expansion. Thus, the abutment backfill limitation was recognized based on friction angle and soil density which correspond to load and resistance of backfill, respectively. On the other hand, soil layers around supporting piles only resist bridge loads and movement. Characteristics and variations of typical backfill soil properties shown in (Table 5). Density and friction angle of backfill soils of field-tested bridges were all the same, and these parameters were assumed as mean values. For the subgrade modulus, field measurements were examined using abutment displacement and backfill pressure. As mentioned earlier, p-y curves were obtained from AP and shown in Fig. (7).

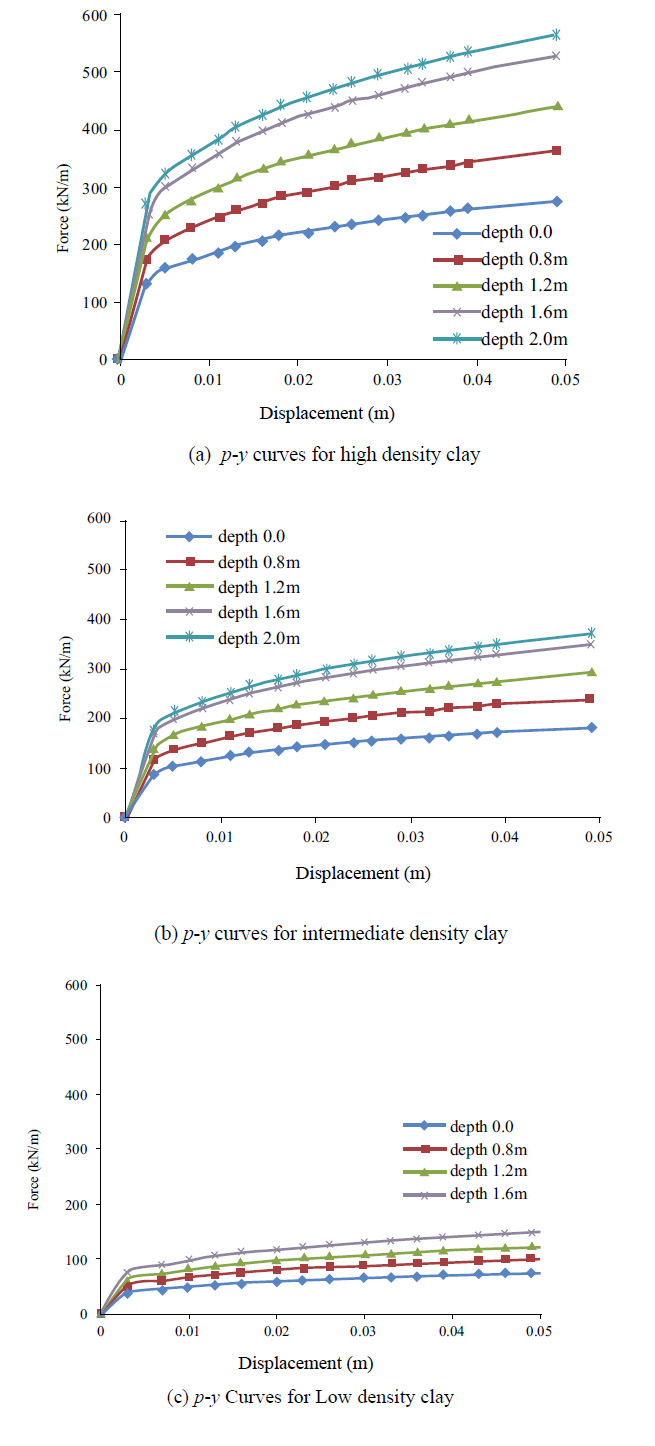
HP 1274 piles with yield strength of 345 MPa were used for the parametric study. In the present study, piles were assumed to be driven up to 18.9 m below the surface. Soil pile interaction properties also considered various overburden pressure and soil properties. Three different high and low values for soil pile interaction settled to the different overburden pressures. The assumed high and low soil stiffness properties for clay are shown in Table 6. Intermediate values were established from the average of high and low values. Furthermore, clay with high, intermediate, and low stiffness p-y curves are shown in Fig. (8).

2.2. Artificial Neural Network Pattern

The unit in each layer (X1, X2, Xn, ..yn) is named neurons, which refers to inputs and output data in the mathematical model. For the most part, a network is trained by changing the weights of the connections between nodes. These weights can be randomly chosen or individually chosen. Usually, a computer program randomly generates values for connection weights. Then, the network is given an input, and it is allowed to process the information through its nodes to produce an output. The input can be raw data or output of other processing elements. The input layer receives data from the outside and sends signals to the subsequent layers. The outside layer interprets signals from the previous layer to produce a result that is transmitted to the outside as the network's understanding of the input data. Based on this advantage of information processing, neural networks can easily exploit the massively parallel local processing and distributed storage properties in the brain accepts inputs from single or multiple sources, and produces outputs by simple calculations, processing with a predetermined nonlinear function. In this study, a two-layer hide was trained by using Visual Gene Developer programming language; the training process of the network automatically stops when the generalization of network stops improving and when the mean square error of the validation process tends to increase. For the two hidden layers, 10 and 5 neurons respectively were set; the number of neurons was determined based on many preliminary simulations in which the number of neurons was varied and two different analyses were carried out. In the first one, the number of neurons of the second hidden layer was fixed while one of the first hidden layers was varied. In this case, the best simulation was obtained with 10 neurons in the first hidden layer. The next analysis was carried out by fixing 10 neurons in the first layer and by varying the ones in the second one. In this case, the best regression was obtained with five neurons in the second hidden layer. The ANN with 10 and 5 neurons in the first and the second layers respectively provided the higher value and lowest average error, soil pile interaction a higher computational time for the training being required.

Several input parameters were chosen to provide for the training of the network, specifically the bridge span, backfill height, stiffness of soil behind abutment and soil stiffness around pile. Each input neuron represents a separate attribute in the train datasets station for example from the bridge span. The number of input variables is 4, consisting of bridge span, backfill height, soil stiffness behind abutment, and soil stiffness around piles. The number of outputs is five, consisting of pile lateral force, pile displacement, pile head moment, girder axial force, and abutment moment. The training setting for two hidden layers. In this parametric study, three levels of span 18.3, 35.4 and 64.5 were selected to train to the prediction of response with another longer span (i.e., 123.6 m and 245 m).

3.1. FE Results

The domain is selected in line with the proper range. For the purpose of determining the effect of bridge span on critical lateral displacement of bridge following time history analysis under seismic loads, three spans were selected as shown in Table 8. The lateral displacement shown by the change in the span of the bridge. Time history analysis was applied in all pile displacement cases and pile displacement for three groups of spans. In Fig. (9a), three bridges with the same 18.3 m span were analyzed and the lateral displacements were compared together. Bearing in mind the conditions of equality to stiffness of backfill, case 2 with intermediate stiffness clay around the pile shows better performance and with less lateral displacement. This process is repeated in Fig. (9b & c), which illustrates that generally the best performance is related to clay with low stiffness. If lateral displacement provides a favorable condition, IAB has better performance.

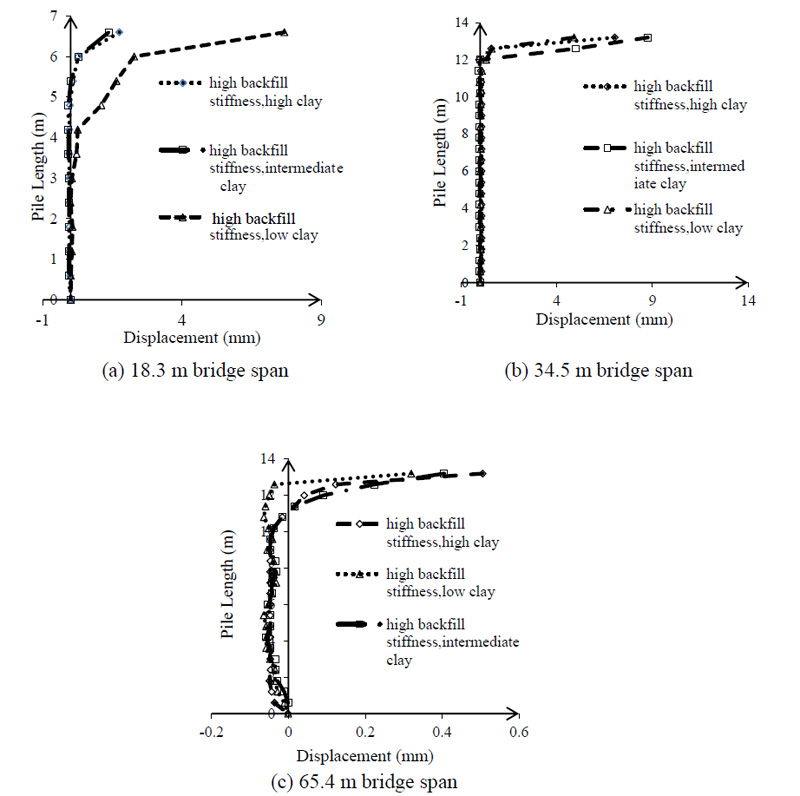
The maximum average positive moment, increased the studied cases with span 18.3 m to 32.13 kN-m, whereas for span 34.5 m it was 42.38 kN-m and for span 65.4 m it was 71.13 kN-m. The maximum average negative moment, and increase in the studied cases with 18.3 m was -30.5 kN-m, 34.5 m it was -42.38 kN-m, while for 65.4 m span it was -79.13 kN-m. Most of the pile-yielding cases were IABs with 65.4 m. With the increase in bridge span, both compressive and tensile girder axial forces, increase considerably. The maximum average compressive girder axial force increases between the studied cases with span 18.3 m and 65.4 m were 389.7 kN and 795.1 kN, respectively. Also, the maximum average tensile girder axial force increases between the studied cases with span 18.3 m and 65.4 m were 250.0 kN and 522.1 kN, respectively. As bridge span increases, both positive and negative girder bending moment at the abutment, significantly increases. The average positive moment increase in the studied cases with span 18.3 m was 366.5 and for 65.4 m it was 548.8 kN-m. In addition, the average negative moment increase in the studied cases with span 18.3 m was -268.6 kN-m and for 65.4 m it was -591.7 kN-m. In Table 9, the results of the time history are reviewed.

Considering the conditions of equality to the stiffness of soil around the pile with high stiffness, backfill stiffness has an important effect on lateral displacement. Best performance is related to high stiffness backfill with high clay around the pile. The backfill stiffness is rarely influential on pile lateral force. The backfill stiffness does not affect the efficacy of the pile bending moment, as it does not have any influential effect on the girder bending moment. The domain of stiffness soil around pile changes in this parametric study is from high to low stiffness in properties that are determined in detail in Table 10.

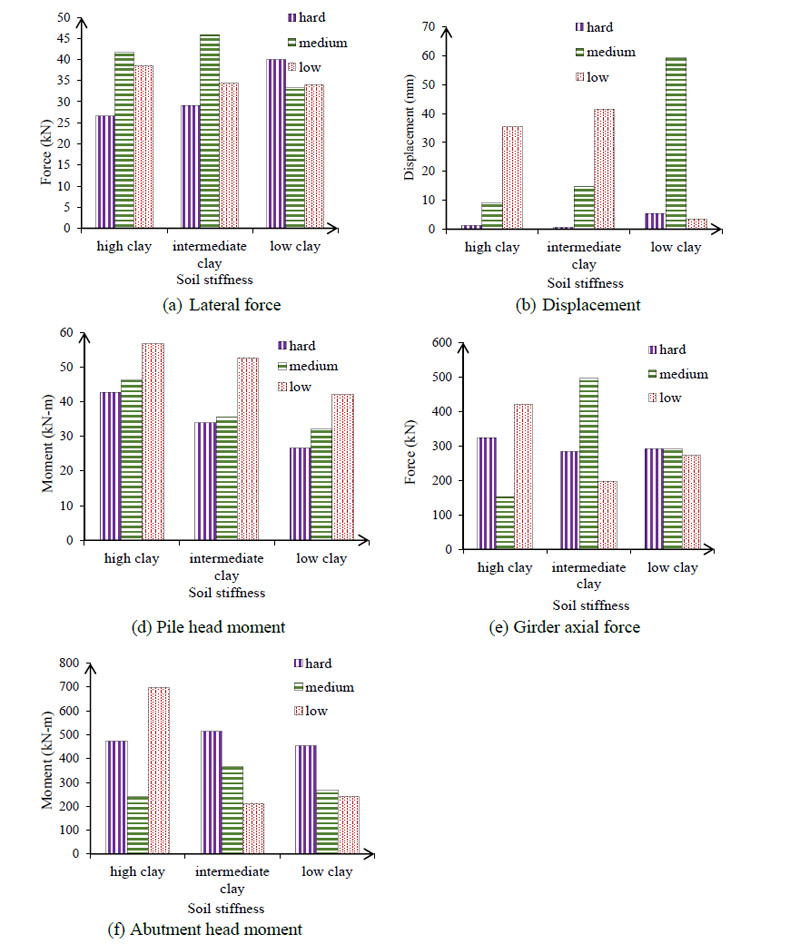
The results of the time history analysis are presented in Table 11. Fig. (10) shows the absolute value of outputs relative to the seismic load applied in the longitudinal direction as a parametric modeling case considered 34.5 m span and 4.6 m height of backfill by stiffness soil around the pile and backfill stiffness. When soil stiffness around the pile is high and subjected to ground motions, the maximum lateral force in the longitudinal direction obtained is 26.6 kN for the case where the backfill stiffness is hard. However, for clay stiffness that is intermediate and low analyzed using the same ground motions and scales and including the soil pile interaction behavior in the structural models, maximum lateral force is obtained as 29.12 and 40 kN respectively. The differences between maximum displacements obtained from high, intermediate and low clay stiffness around pile are 37.8% and 85.6% respectively as shown in Fig. (10b). The upper level represents the maximum envelope and the lower level is the minimum envelope of outputs for 81 sets that were modeled.

3.2. ANN Results

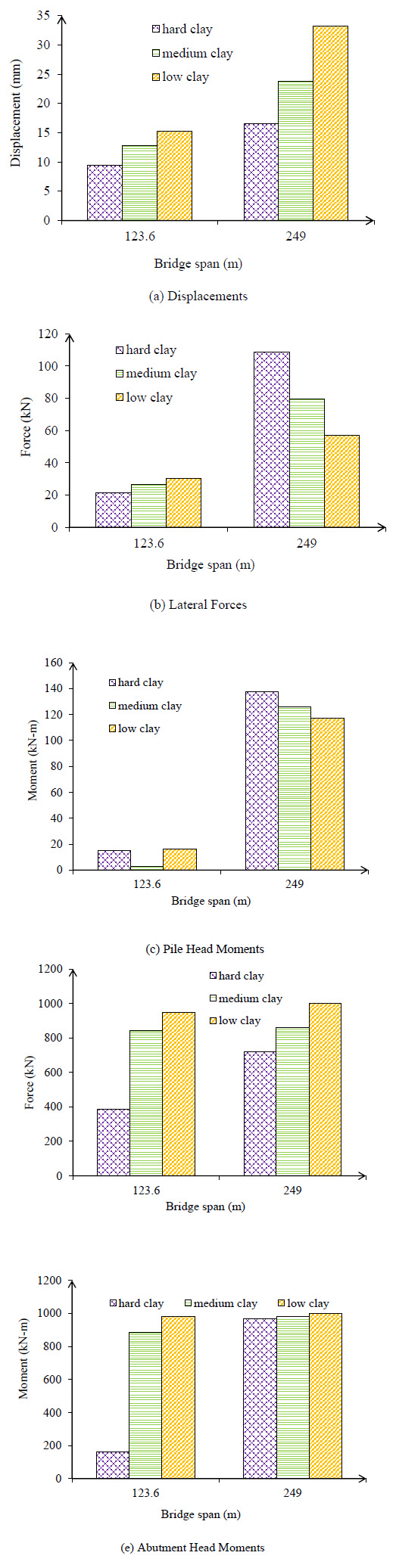
ANN (i.e., Visual Gene Developer) was used to perform response prediction for pile lateral force, pile displacement, pile head moment, girder axial force and abutment moment. Fig. (11) shows the absolute value of outputs forecast relative to the seismic load applied in the longitudinal direction including the stiffness soil around the pile. As shown in Fig. (11a), the absolute value of displacement with considered stiffness of soil around pile for 123.6 m span with hard, medium and low-density clay, is 9.42, 12.78, 15.32 mm respectively and for 246 m span is16.56, 23.76, 33.20 mm. When the bridge span is increased, pile lateral force significantly increases. The lateral force for 249 m span with hard stiffness soil around the pile predicted by ANN was 108.84 kN. As bridge span increases, both compressive and tensile pile head moment, considerably increase (Fig. 11b). With a comparison between two bridge lengths, the girder axial force increases between the studied cases with a span of 123.6 m and 249 m and the absolute values for medium clay are 26.86 kN and 108.84 kN, respectively. The absolute value for girder axial force changes 336.79 kN between 123.6 and 249 m span for hard clay (Fig. 11d). As bridge span increases, both positive and negative abutment head moment, increases as depicted in Fig. (11c). Based on the parametric results as input to Visual Gene Developer, the abutment head moment is forecast at 162.63 kN-m for 123.6 m span and 968 kN-m for 249 m span in the hard clay. The results of the Artificial Neural Network analysis are presented in Table 12.

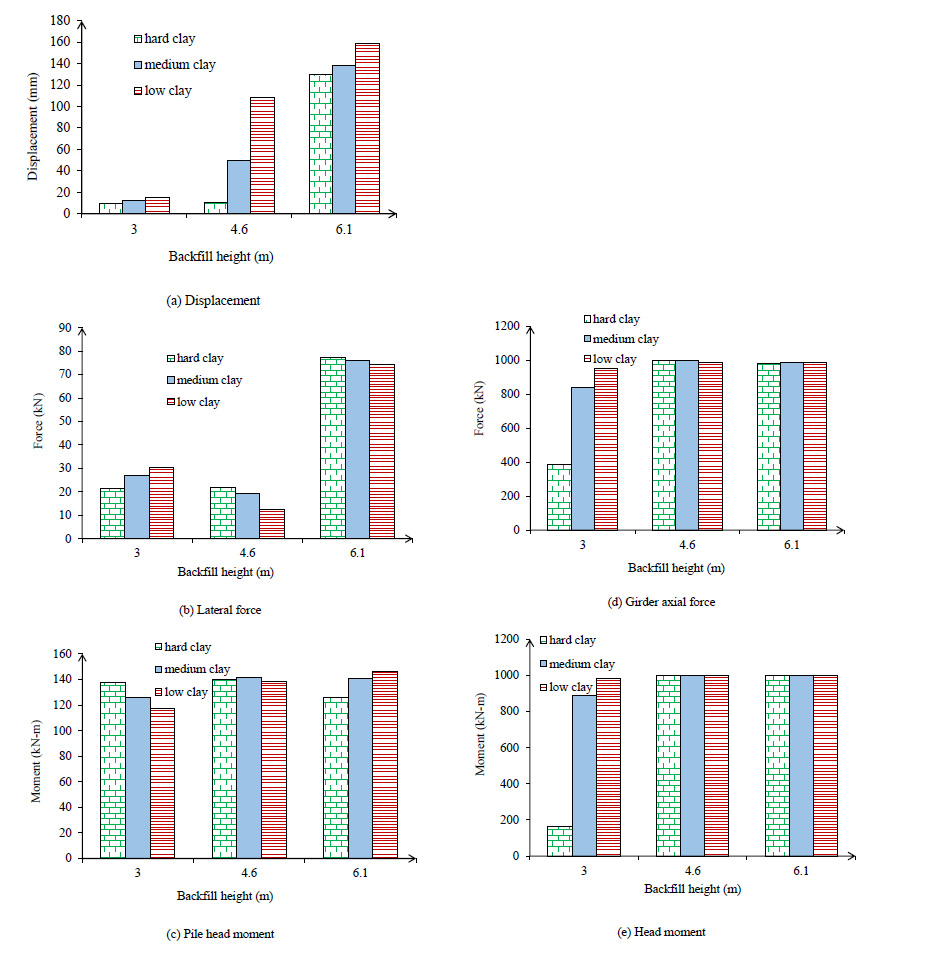
3.2.1. Prediction of Critical Response for Backfill Height

As shown in Fig. (12a), by changing the height of the abutment with the company span of the bridge, structural stiffness increased, but this factor is not related to the lateral displacement. For 123.6 m span when the backwall height is 3.0 m subjected to ground motions, the maximum lateral displacement in the longitudinal direction is found to be 12.78 mm for the case where stiffness soil around the pile is hard. However, for backwall heights 4.6 and 6.1 m and using the same ground motions and including the soil pile interaction behavior in structural models, lateral force is predicted as 8.16 and 139.99 mm respectively. The pile lateral force for 123.6 m span was predicted for 3.0 m height of backfill 21.27 kN, for 4.5 m is 21.63 kN and for 6.1is 77.23 kN. Pile head moment for 123.6 m span is illustrated in Fig. (12b). In this figure, changing backwall height from short to tall makes no meaningful change in the bending moment value. The pile head moment for 123.6 m and 3.0 m height with hard density soil around pile forecast is 15 kN-m. The girder axial force for 123.6 m span and hard clay around the pile is 384.18 kN. This comparison is between 123.6 m span and parametric study cases with 18.3, 34.3 and 65.4m spans. With the comparison between ANN results and time history analyses in the parametric study, backfill height influences abutment head moment. An increase of backfill height decreases abutment head moment and the moment decrease between 3.0 m and 6.1 m was 85 kN-m in 123.6 m span.

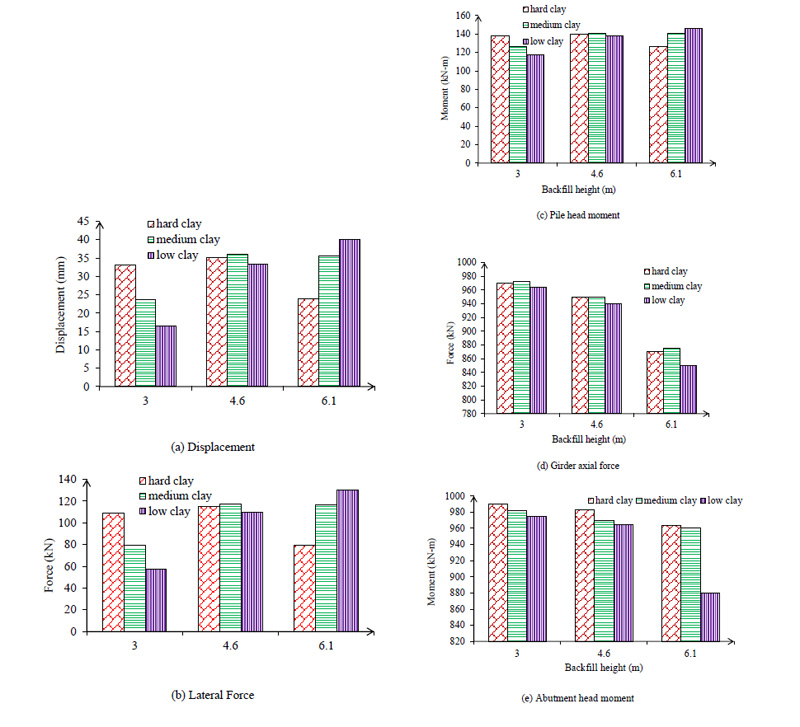
The pile lateral displacement predicted for 249 m span and 3.0 m height of backfill is 33.20 mm, for 4.5 m is 35.12 mm and for 6.1 is 23.81 mm. In 249 m length similar to 123.6 m height of abutment is not related to lateral force. For 249 m spans as shown in Fig. (13a) when backwall height is 3.0 m subjected to ground motions, the maximum lateral force in a longitudinal direction obtained is 108.84 kN for the case where stiffness soil around pile is hard. However, for backwall heights 4.6 and 6.1 m and using the same ground motions and including the soil pile interaction behavior in structural models, lateral force is predicted at 114.77 and 79.64 kN respectively. Prediction of pile bending moment for 249 m span showed no relation between pile head moment and backfill height. The pile moment for 3.0 m height with hard density soil around pile is 137.71 kN-m Fig. (13b). The girder axial force predicted for 249 m span and hard clay around pile is 999.97 kN. This comparison is between 249 m span and parametric study cases with 18.3, 34.3 and 65.4m spans. The maximum girder axial force reduction between 6.1 m and 3.0 m was -152 kN (see Fig. 13(c)). With a comparison between ANN results and time history analysis in the parametric study, backfill height influences abutment head moment as shown in Fig. (13d). An increase in backfill height decreases the bending moment at the abutment and the bending moment decrease between 3.0 m and 6.1 m predicted 114.02 kN-m in 249 m span.

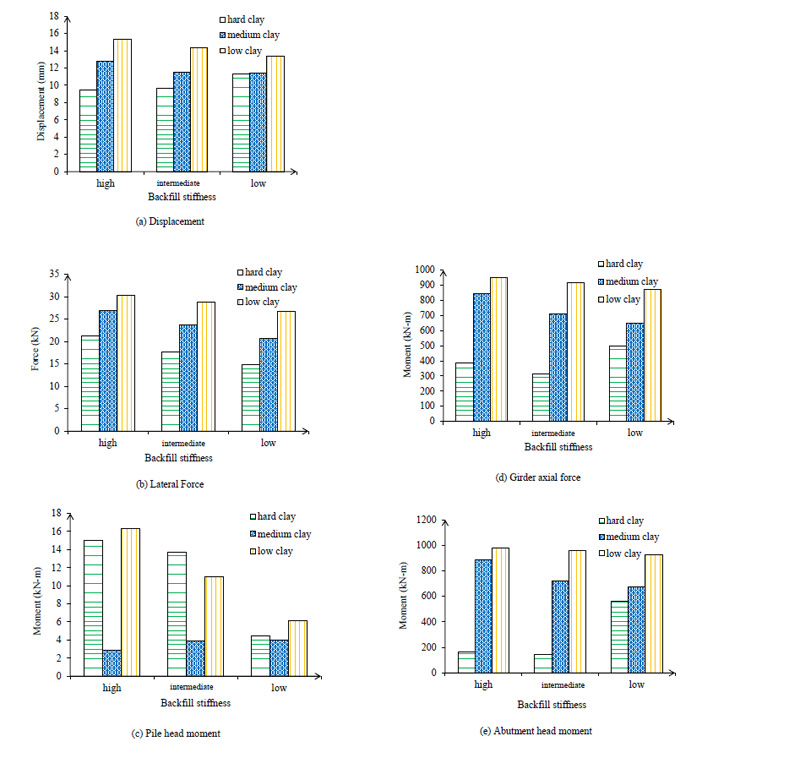
3.2.2. Prediction of Critical Response for Backfill Stiffness

For 123.6 m span, lateral displacement, lateral force, bending moment and abutment moment are shown in Fig. (14). The pile lateral force change between low and high stiffness was 3.94 kN. Backfill stiffness has a low influence on pile lateral force at the pile head. The pile head moment change between low and high stiffness was predicted at 1.16 kN-m. The girder axial force forecasted with low stiffness backfill and low clay around the pile was 800 kN. The girder axial force predicted by ANN for 123.6 m was 910 kN (Fig. 14d). As mentioned earlier, backfill stiffness does not influence abutment head moment which (Fig. 14e) confirms. Girder bending moment forecasted for low stiffness backfill with low clay around pile was 880.23 kN-m.

For 249 m span prediction of lateral displacement, lateral force, bending moment and abutment moment are shown in Fig. (15). As predicted by ANN and depicted in (Fig. 15a), backfill stiffness has an influence on pile lateral force. The pile lateral force predicted with high clay stiffness around the pile and high compacted backfill was 33.82 kN. Also, backfill stiffness has a high influence on pile lateral force at the pile head (Fig. 15b). As shown in Fig. (15d) the girder axial force forecasted between low and high was 73.95 kN. Girder moment forecast with high stiffness around pile was 1000 kN-m for 249 m length (Fig. 15e).

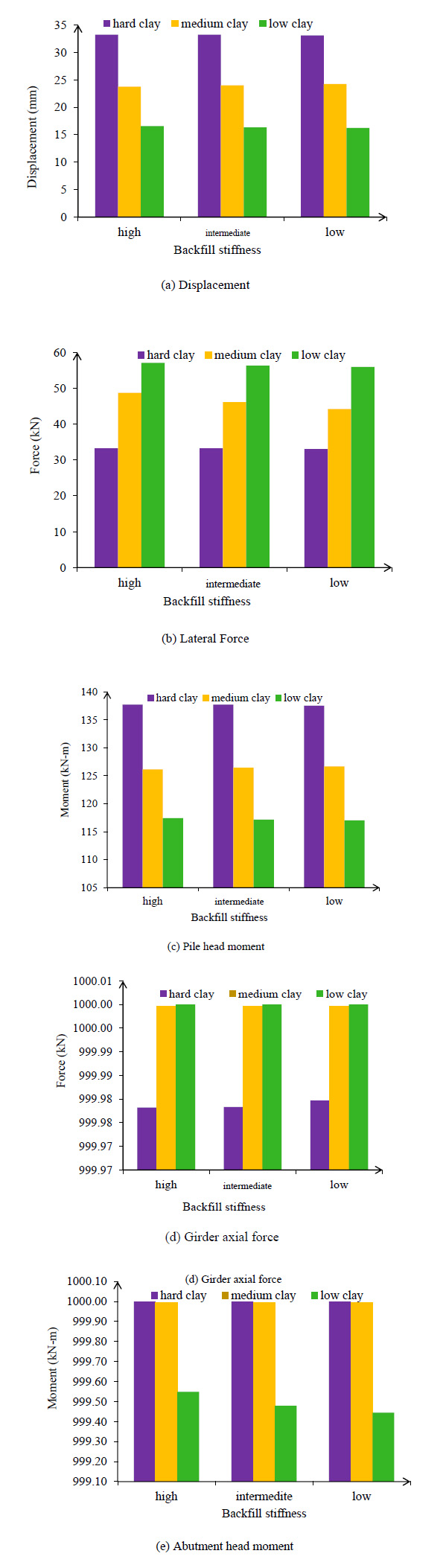
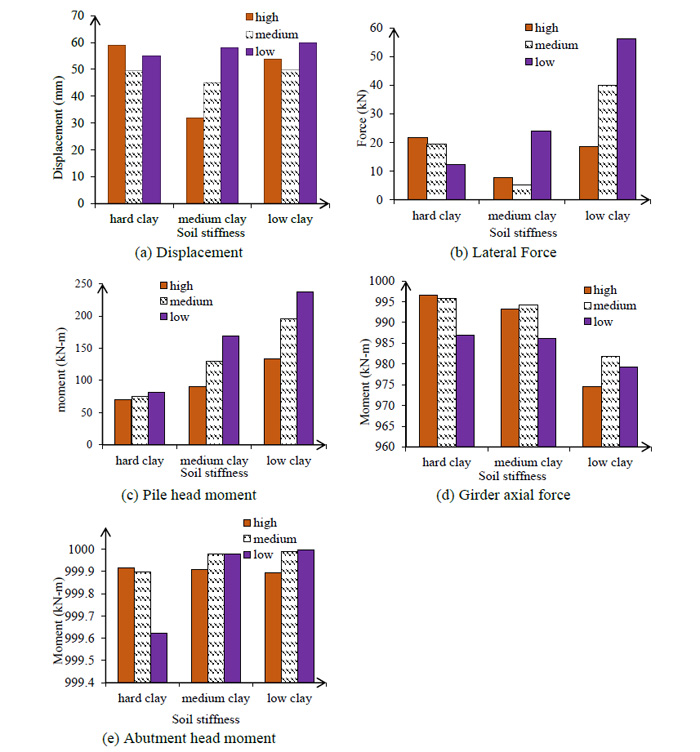
3.2.3. Prediction of Critical Response for Soil Stiffness Variable

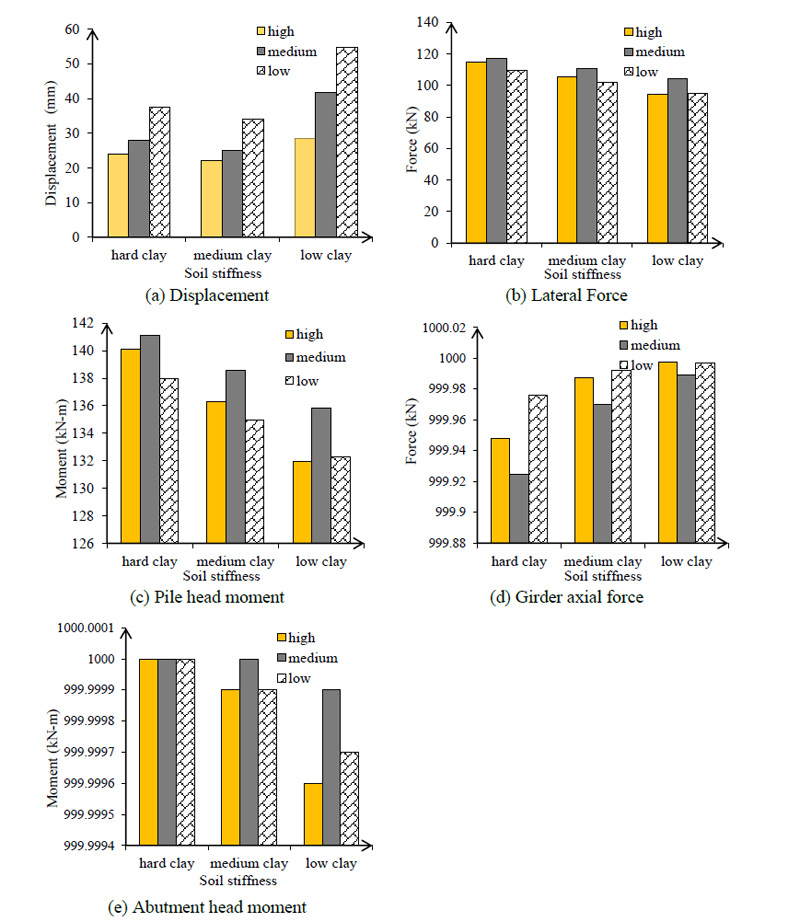
The effect of soil stiffness around pile on the critical response of bridge after ANN analysis, 4.6 m backfill height was selected for IAB (Figs. 16 and 17). The results show that soil stiffness around piles reduces pile lateral displacement. The absolute lateral force prediction for low clay backfill around the pile was 58.07 kN (Fig. 16b). The pile head moment increase between low and high stiffness was 160.23 kN-m for 123.6 m length (Fig. 16c). The maximum pile lateral force addition with high clay stiffness was 118 kN (Fig. 17c) and the pile head moment increase between low and high stiffness was 9 kN-m for 249 m length (Fig. 17c). As shown in Fig. (17d) the maximum girder axial force predicted by ANN was 999.92 kN. Finally, the bending moment predicted between low and high clay stiffness was 1000 kN-m.