A Comparative Assessment of Regularized Regression Techniques for Modeling the Mechanical Properties of Rubberized Concrete
Abstract
Background:
Over the last few decades, many researchers have investigated the properties and behavior of concrete mixtures incorporating rubber-based solid wastes as a partial substitution of natural aggregates. Within this context, they have conducted experimental studies and developed numerical models that simulate the nature of rubberized concrete. Some of these mathematical simulations were intended to provide a rapid mixture of proportioning approaches and property estimation methods. Currently, it is believed that regression analysis provides an effective tool to simply construct a mathematical expression that models a set of data. For that reason, multiple linear regression was extensively utilized in predicting rubberized concrete properties in the literature. However, the performances of regularized regression analysis approaches were not evaluated even though they provide better alternatives to traditional regression methods in terms of controlling the overfitting issue.
Objective:
This study aims to assess the performance of Ridge, Lasso, and elastic net regression models in estimating the compressive and tensile strengths, and modulus of elasticity of rubberized concrete. Additionally, it intends to benchmark their capabilities against the traditional multiple linear regression method.
Methods:
Multiple linear regression, Ridge regression, Lasso regression, ElasticNet regression, Bayesian ridge regression, Stochastic gradient descent, Huber regression, and Quantile regression methods were used in the study.
Result:
In general, the research findings illustrated the superior performance of regression assessment in modeling the mechanical properties of rubberized concrete.
Conclusion:
Indeed rubberized concrete mechanical properties can be better modeled using regularized regression techniques, such as ElasticNet-based SGD compared to traditional methods, such as MLR.
1. INTRODUCTION
Rubber recycling is sometimes referred to as tire recycling because it is mainly used in the tire industry, which generates a tremendous amount of rubber waste [1]. As it is well-known that the decomposition of polymers takes a long time and has significant environmental repercussions, thus governments worldwide have a big challenge in dealing with non-biodegradable waste. The past several decades have seen many studies employing recycled particles in cementitious mixtures to partially replace natural aggregates [2, 3]. Today, the disposal of old rubber tires is considered a major environmental problem [4-6]. The most critical risks related to this process include uncontrolled fires, and other environmental threats and some health issues [7]. In practice, about one billion tires reach the end of their useful life each year, according to the World Business Council for Sustainable Development [8]. The production of rubber tires and rubber goods was 4.89 million tons and 2.68 million tons, respectively, in 2015. It increased by 2% in the rubber products industry and 1% in the manufacture of vehicle tires in 2017 [9]. Over the past several years, there has not been a clear trend in rubber output, but the massive amount of rubber waste makes its disposal an abstruse problem for communities today. As a result, crumb rubber from waste tires is becoming more popular as an alternative building material [3].
Several studies have been undertaken to investigate the possibility of using recycled rubber as partial substituting aggregate in concrete mixtures to obtain what is known as “rubber concrete” [10-12]. Regardless of its environmental importance, another advantage of rubber concrete over standard one is its ability to effectively mitigate shaking intensities that, when used in structural parts, may have a positive influence on vibration performance [13-15]. Besides, it has been shown that replacing natural aggregates with waste rubber will significantly minimize the compressive strength and modulus of elasticity [16-22]. The primary cause of these declines is the substitution of a stronger aggregate with a weaker one [13] and the deterioration of the bond between cement paste and aggregate [23, 24].
In reality, statistics are utilized in the civil engineering field to describe and infer data by developing a measure of influence to indicate connections (correlations) or model relationships (regressions) in the dataset. Multiple studies have been focused on developing numerical models to simulate the behavior of rubberized concrete (RBC). For instance, Topçu and Sarıdemir [25] utilized artificial neural networks to predict the density and workability of RBC. Bachir et al. [26] used the same method to estimate RBC's compressive strength. In contrast, Jalal et al. [27, 28] highlighted the capabilities of multivariable linear and nonlinear regression, adaptive neuro-fuzzy inference system, support vector machine, and genetic programming to model the compressive strength of RBC. Cheng and Cao [29] applied similar methods to estimate RBC's splitting tensile strength. Habib and Yildirim [24] adopted multivariable linear regression to predict the dynamic properties of RBC. Hence, multivariable regression analysis addresses several independent variables whose values are known to estimate a single outcome variable because of its simplicity [30]. In contrast, a neural network is more accurate yet complex and hardly applied by practicing engineers on a daily basis for estimating RBC characteristics [24].
There are many versions of regression analysis in the literature, including the improved variants of the multivariable linear regression. The importance of these modified methods comes from their ability to penalize the developed model for enhancing its performance. Additionally, they can overcome specific overfitting issues, including the interaction among the input variables, which forces the analysis of variance to eliminate correlated parameters (the case of RBC mixtures where the rubber content is related to coarse and fine aggregates). Consequently, the regularized regression analysis techniques are a better fit for the case of estimating the mechanical properties of RBC. However, the capability of these methods and their performances in predicting RBC properties have not been investigated before. Moreover, most previous studies have focused on predicting the compressive strength of RBC and rarely investigated other properties. As a result, this study evaluates the performance of various regression analysis techniques with regularization capabilities to predict compressive strength, splitting tensile strength, and modulus of elasticity. Besides, the findings will all be benchmarked against the MLR method as it is one of the most adopted methods in the literature.
2. MATERIALS AND METHODS
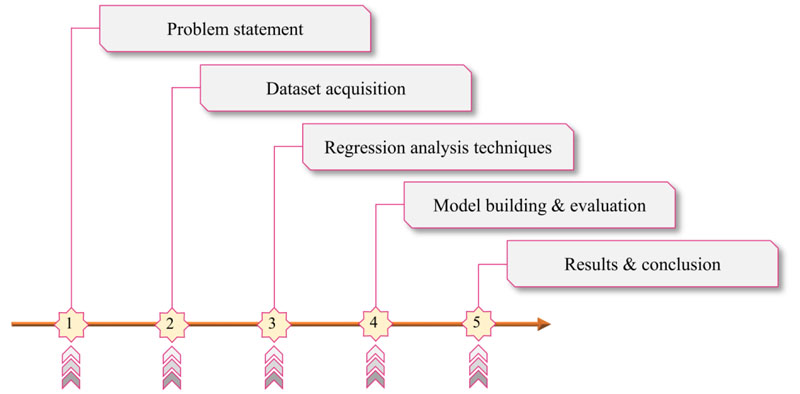
Concrete is a fine (sand) and coarse (either naturally occurring or crushed rock) aggregate mixed with cement paste. On the other hand, worn tires are deemed a severe global ecological and environmental issue. Recent years have seen an increase in interest among researchers in the recycling of scrap tires and the reuse of rubber derived from crushed tires. Many methods for recycling discarded tires were suggested as part of waste management efforts, for instance, incorporating rubber into concrete as an aggregate substitute in the building industry [31]. From an environmental standpoint, using rubber obtained from old tires in concrete mixes has become the preferred solution to reduce the number of rubbish tires and deliver a source of eco-friendly concrete [32, 33]. From a technical perspective, adding recycled-tire rubber particles into cementitious mixtures will enhance concrete's dynamic and durability characteristics [34, 35]. Regression analysis is a statistical approach to predicting associations between a dependent variable and multiple independent ones. In the light of the previous background, Fig. (1) indicates the general methodology adopted in this research for evaluating concrete's mechanical and durability properties with waste rubber based on regularized regression analysis methods.
2.1. Dataset Acquisition
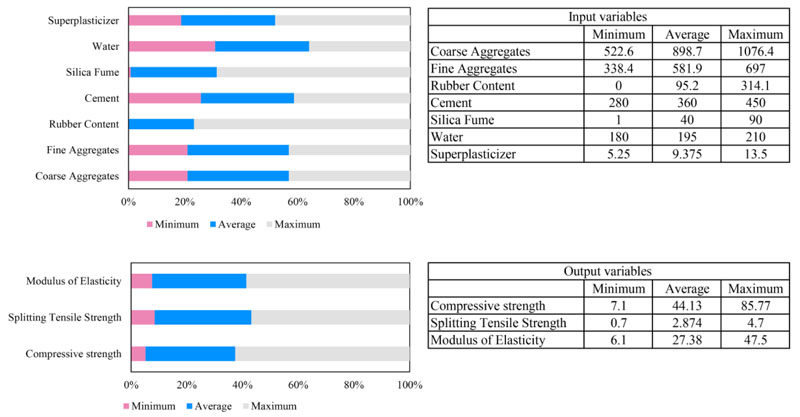
This research aims to quantify rubberized concrete's elastic modulus and compressive and splitting tensile strengths. The dataset was assembled in an experimental database from a previous study to construct numerical models of rubberized concrete properties across a wide range of rubber constitutions [21]. The descriptive statistics of the dataset's characteristics are summarized and organized in Fig. (2). The contents of rubber particles are directly related to the amount of coarse and fine aggregates (Fig. 3), which would raise several issues during the development of a multiple linear regression model.

2.2. Regression Analysis Methods
In statistical analysis, regression techniques are often applied to estimate the risk of a probable outcome [36]. Overfitting occurs when typical regression approaches are utilized for a set of candidate variables to construct a model, generating an overestimation of the model's performance when using the included variables to describe observed variability [37]. The algorithm tends to underperform when it comes to predicting high-risk events. These issues may be addressed using different (penalized or regularization) regression methods [38]. Multiple linear regression employs many explanatory variables to estimate the result of a response variable. Achen [39] discussed its mathematical algorithm, as shown in Eq. 1.
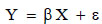 |
(1) |
Where,
Y = [y1, K, yn]T vector of the dependent variables;
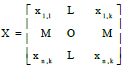 matrix of the independent variables for n measurements and k inputs;
matrix of the independent variables for n measurements and k inputs;
β = [β1, K, βK]T vector of model's coefficients to be predicted;
ε = [ε1, K, εK]T vector of random error;
Ridge regression is a procedure for predicting multivariable regression coefficients when strongly correlated observations are present. As a result, this method is more likely to estimate RBC characteristics from its components better than multivariable linear regression. by considering Eq. 1, the standard least-squares solution of the β coefficients is shown in Eq. 2, in which 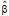 is the best linear unbiased estimate of β.
is the best linear unbiased estimate of β.
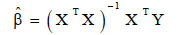 |
(2) |
On the other hand, Hoerl and Kennard [40] developed a ridge regression model to address the issue of multicollinearity by computing coefficients β using Eq. 3 for strongly correlated independent variables.
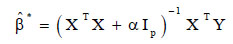 |
(3) |
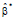 expresses the ridge estimator, α > 0 is the complexity parameter that regulates shrinkage and ensures
expresses the ridge estimator, α > 0 is the complexity parameter that regulates shrinkage and ensures 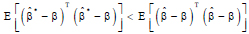 and IP represents the identity matrix.
and IP represents the identity matrix.
Besides, Ridge regression handles some of the drawbacks in traditional least-squares. It imposed a penalty on the size of the coefficients to reduce a penalized residual sum of squares, as given in Eq. 4. Hence, ridge regression employs the squared euclidean norm 12 regularization procedure to penalize the coefficient vector.
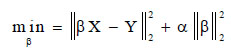 |
(4) |
Lasso regression is a linear predictor of dispersed coefficients. According to its disposition to select solutions with fewer non-zero coefficients, it is helpful in some settings, effectively decreasing the number of characteristics on which the delivered result is reliant [41]. Mathematically, it composes of a linear algorithm with an added regularization term. The objective function to minimize is indicated in Eq. 5, where α is a constant value and 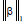 denotes the absolute norm 11 of the coefficient vector.
denotes the absolute norm 11 of the coefficient vector.
 |
(5) |
ElasticNet regression is a linear method trained with both 11 and 12 norm regularization of the coefficients to enable learning a scattered algorithm in which few weights are non-zero such as Lasso, while keeping the Ridge’s regularization features [42]. On the other hand, ElasticNet is beneficial when several properties are correlated. The objective function to minimize is determined in Eq. 6, where ρ is a parameter inserted to control the convex combination of 11 and 12.
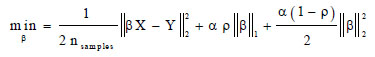 |
(6) |
Bayesian regression is a method used to develop linear regression models by utilizing Bayesian inference where the errors εi : N (0, 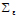 ) are independent and normally distributed. Additionally, it has a prior probability distribution of variables with the likelihood function given in Eq. 7 to find the posterior probability distribution.
) are independent and normally distributed. Additionally, it has a prior probability distribution of variables with the likelihood function given in Eq. 7 to find the posterior probability distribution.
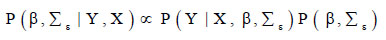 |
(7) |
In Bayesian ridge regression (BR), on the other hand, the regression problem is modeled using a probability distribution to avoid multicollinearity (Zhang et al., 2019). It is possible to write the objective function of this model, as shown in Eq. 8. The priors over parameter α and the precision λ are defined using gamma distributions and are predicted jointly with β in the model’s fitting stage.
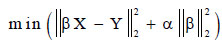 |
(8) |
Stochastic gradient descent (SGD) is an easy and effective method for fitting linear regression models. It is currently considered a beneficial method for fitting models with many features. The loss gradient is predicted for each sample at once and then updated with a decreasing strength schedule. Within the prediction of this model, three types of regularizers can be adopted, including 11 , 12, and ElasticNet. However, the SGD model in this study adopts the ElasticNet in the penalty function for estimating the mechanical properties of RBC.
Huber regression is a method of developing linear regression that is sensitive to outliers by optimizing β and σ values for the samples’ squared loss when 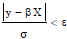 and for their absolute loss when
and for their absolute loss when 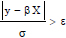 . This step ensures that the errors in the model are highly affected by the existing outliers. The objective function used for this type of model is defined in Eq. 9.
. This step ensures that the errors in the model are highly affected by the existing outliers. The objective function used for this type of model is defined in Eq. 9.
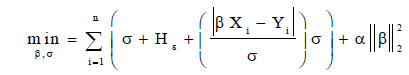 |
(9) |
Where, Hε is given by the following equation:
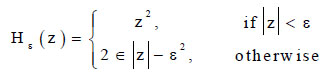 |
(10) |
Quantile regression is a type of linear regression that predicts the medium quantiles of a given y conditional on X and uses the ordinary least squares to predict the conditional mean. Accordingly, its output is the qth quantile for any value of q ranging between 0 and 1. The objective function used in this technique is defined in Eq. 11.
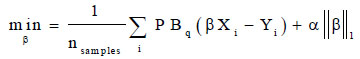 |
(11) |
Where, PBq is the pinball (linear) loss given by the following mathematical expressions:
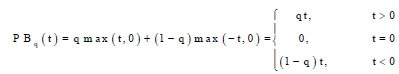 |
(12) |
Indeed, the pinball loss herein is linear for residuals only, and thus, this technique is better for handling outliers than the squared error prediction of the mean.
2.3. Model Development and Hyperparameters Tuning
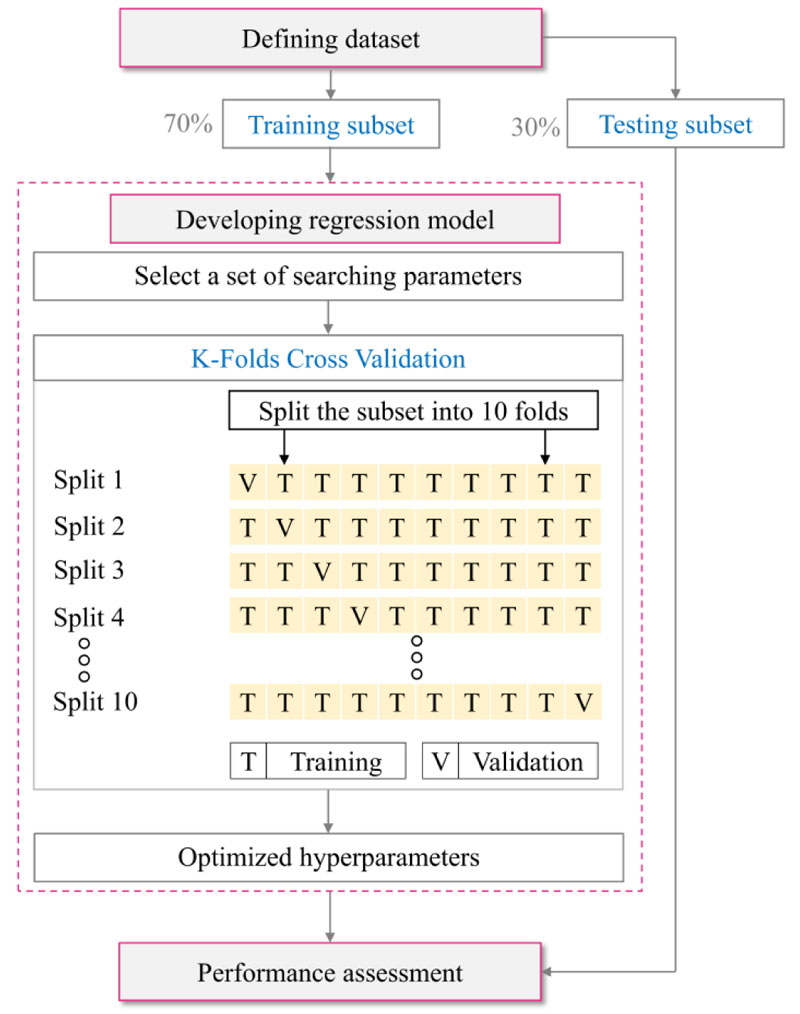
The chosen hyperparameter values have a significant influence on regression analysis results. This article utilized a grid search procedure with k-fold cross-validation to improve the method hyperparameters during the training phase. Fig. (4) illustrates a proposed methodology for concocting regression models in which the dataset is divided into two groups: 70% training and 30% testing data. The appropriate parameter is selected using a cross-validation method with 10-folds repeats. The final tuned algorithm implementation is evaluated by comparing the outcomes of different scoring parameters on the test dataset after the hyperparameters of each technique have been decided.
2.4. Models' Performance Evaluation
Statistical measures and visual representations are adopted to analyze regression techniques' performance. The goodness-of-fit was checked using the coefficient of determination, by using Eq. 13. The root mean square error (RMSE), by Eq. 14, and mean absolute error (MAE), by Eq. 15, were used for the error analysis.
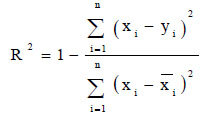 |
(13) |
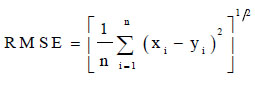 |
(14) |
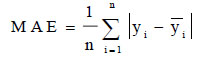 |
(15) |
xi is the measured value, 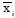 is the mean of the measured values, yi is the predicted value,
is the mean of the measured values, yi is the predicted value, 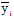 is the mean of the predicted values, and n is the number of observations.
is the mean of the predicted values, and n is the number of observations.
3. RESULTS AND DISCUSSION
3.1. Compressive Strength
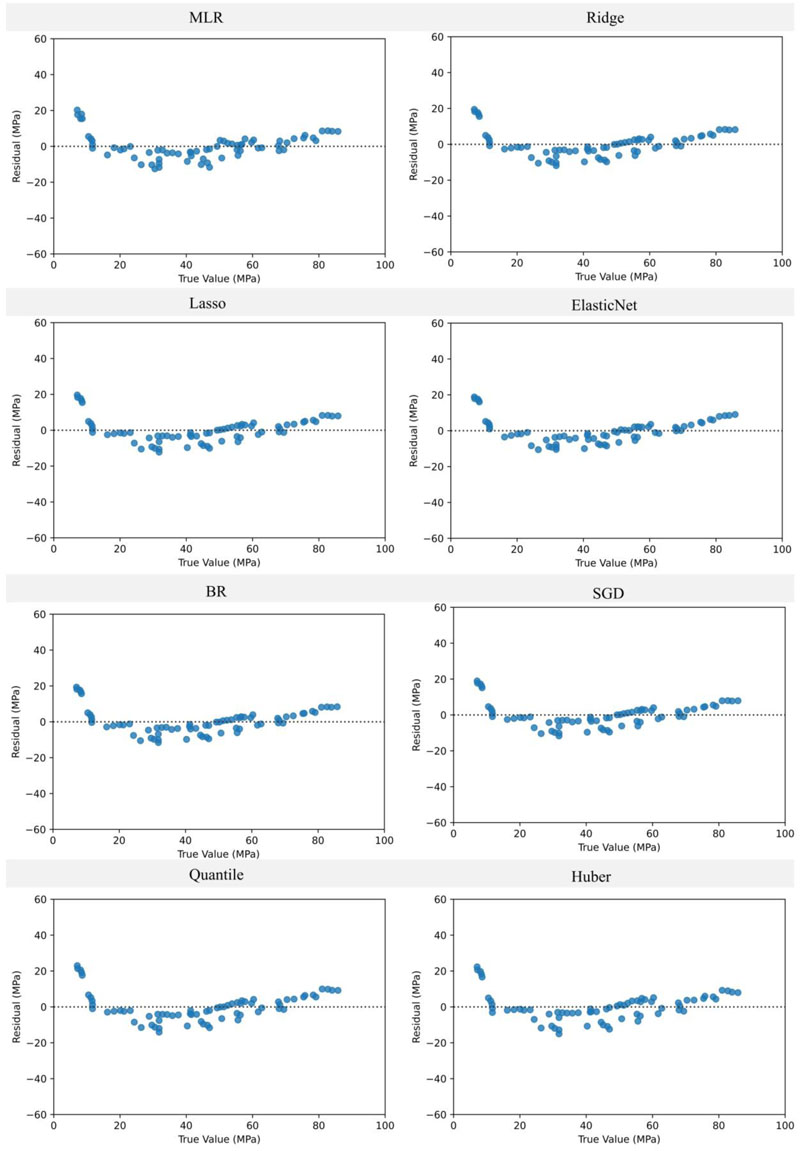
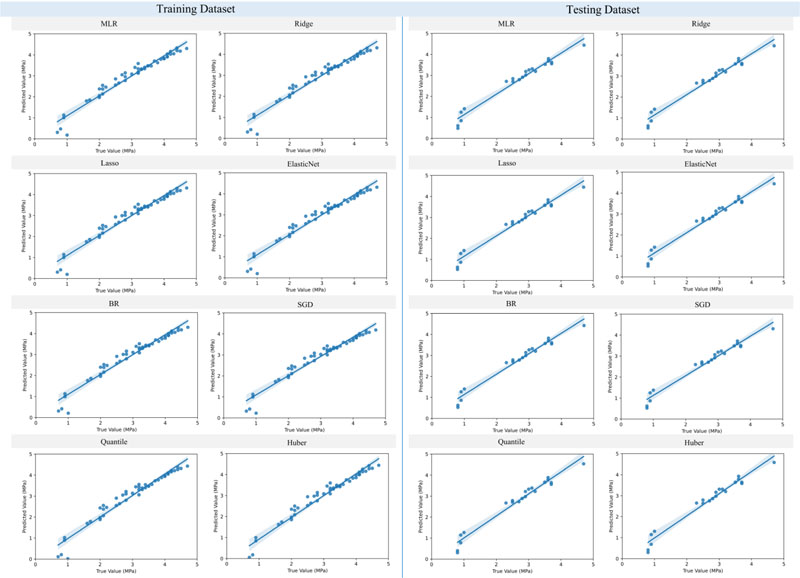
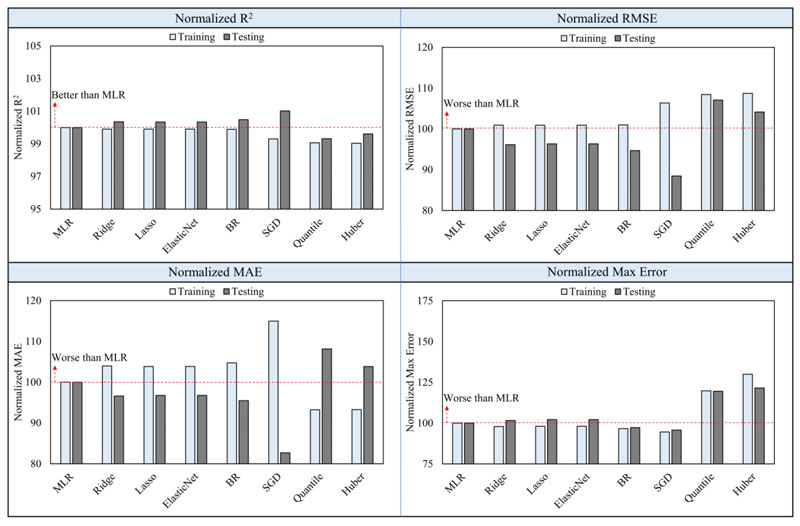
Indeed, the compressive strength of concrete is a critical parameter for designing structures [43, 44]. This section is intended to evaluate the applicability of the abovementioned eight different regression approaches in terms of suitability and accuracy in modeling RBC compressive strength. The estimation results for the training and testing datasets are similar across most models, as shown in Fig. (5). The residual plots of the prediction outcomes are depicted in Fig. (6), in which most regression models tend to provide similar findings with slight variations among them. Table 1 shows the model's performance, and it is clear that the MLR model had the highest coefficient of determination compared to other techniques for the training dataset while having a lesser one when it came to the testing dataset. Also, the Quantile and Huber methods produced the best MAE values in the training case, while the worst was for the testing scenario. This observation is attributed to overfitting issues in these models. In contrast, the ElasticNet and SGD models showed the lowest error values in training but had the highest ones in the testing case, which means that these models are the best regarding the overfitting issue. The RMSE of ElasticNet and SGD was 8.41% and 9.01% lower than the MLR on the testing dataset, but the MAE was reduced by 6.1% and 8.8%, respectively.

| Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (MPa) | MAE (MPa) | Max Error (MPa) | R2 | RMSE (MPa) | MAE (MPa) | Max Error (MPa) | |
| MLR | 0.90 | 6.99 | 5.60 | 16.93 | 0.86 | 7.73 | 6.25 | 14.76 |
| Ridge | 0.90 | 7.11 | 5.71 | 16.14 | 0.88 | 7.16 | 5.96 | 13.45 |
| Lasso | 0.90 | 7.11 | 5.68 | 16.33 | 0.88 | 7.18 | 6.02 | 13.44 |
| ElasticNet | 0.90 | 7.17 | 5.90 | 15.23 | 0.88 | 7.08 | 5.70 | 13.44 |
| BR | 0.90 | 7.12 | 5.74 | 15.94 | 0.88 | 7.13 | 5.90 | 13.45 |
| SGD | 0.90 | 7.14 | 5.89 | 14.73 | 0.88 | 7.03 | 5.87 | 12.18 |
| Quantile | 0.88 | 7.92 | 5.21 | 26.21 | 0.82 | 8.76 | 6.73 | 22.27 |
| Huber | 0.89 | 7.59 | 5.26 | 23.37 | 0.83 | 8.29 | 6.54 | 19.22 |
3.2. Splitting Tensile Strength
The potential of regularized regression techniques will be compared in this section to predict the splitting tensile strength of RBC. Fig. (7) highlights the analysis results, and Fig. (8) depicts the residual plots of the outputs. Similar to the preceding part, Figs. (7 and 8) demonstrate a moderate shift in the results of the estimating model. The coefficients of determination listed in Table 2 for the training and testing datasets are significantly high regardless of the used regression model. The errors analysis of the algorithms has shown that the SGD generated the lowest values with an 8.7%, 20%, and 2.5% reduction in the RMSE, MAE, and Max error, respectively, compared to the MLR. In contrast, the outcomes of the Ridge, Lasso, and ElasticNet were identical, and the Quantile and Huber methods had the worst capabilities for both the training and testing cases. Thus, it can be seen that the SGD is the best predictor for the splitting tensile strength of RBC.
| Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (MPa) | MAE (MPa) | Max Error (MPa) | R2 | RMSE (MPa) | MAE (MPa) | Max Error (MPa) | |
| MLR | 0.95 | 0.24 | 0.18 | 0.82 | 0.96 | 0.23 | 0.20 | 0.41 |
| Ridge | 0.95 | 0.24 | 0.19 | 0.80 | 0.96 | 0.22 | 0.19 | 0.42 |
| Lasso | 0.95 | 0.24 | 0.19 | 0.80 | 0.96 | 0.22 | 0.19 | 0.42 |
| ElasticNet | 0.95 | 0.24 | 0.19 | 0.80 | 0.96 | 0.22 | 0.19 | 0.42 |
| BR | 0.95 | 0.24 | 0.19 | 0.79 | 0.96 | 0.22 | 0.19 | 0.40 |
| SGD | 0.94 | 0.26 | 0.21 | 0.77 | 0.97 | 0.21 | 0.16 | 0.40 |
| Quantile | 0.94 | 0.26 | 0.17 | 0.98 | 0.95 | 0.25 | 0.22 | 0.49 |
| Huber | 0.94 | 0.26 | 0.17 | 1.06 | 0.95 | 0.24 | 0.21 | 0.50 |

3.3. Modulus of Elasticity
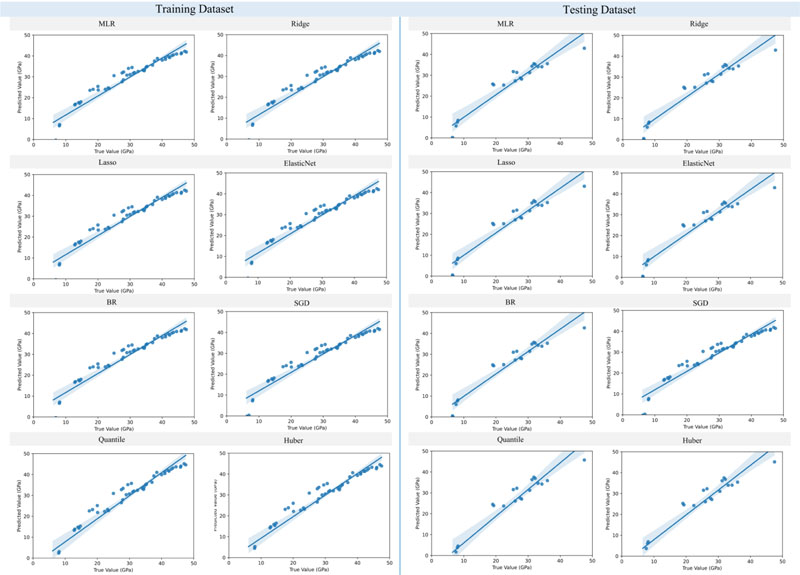
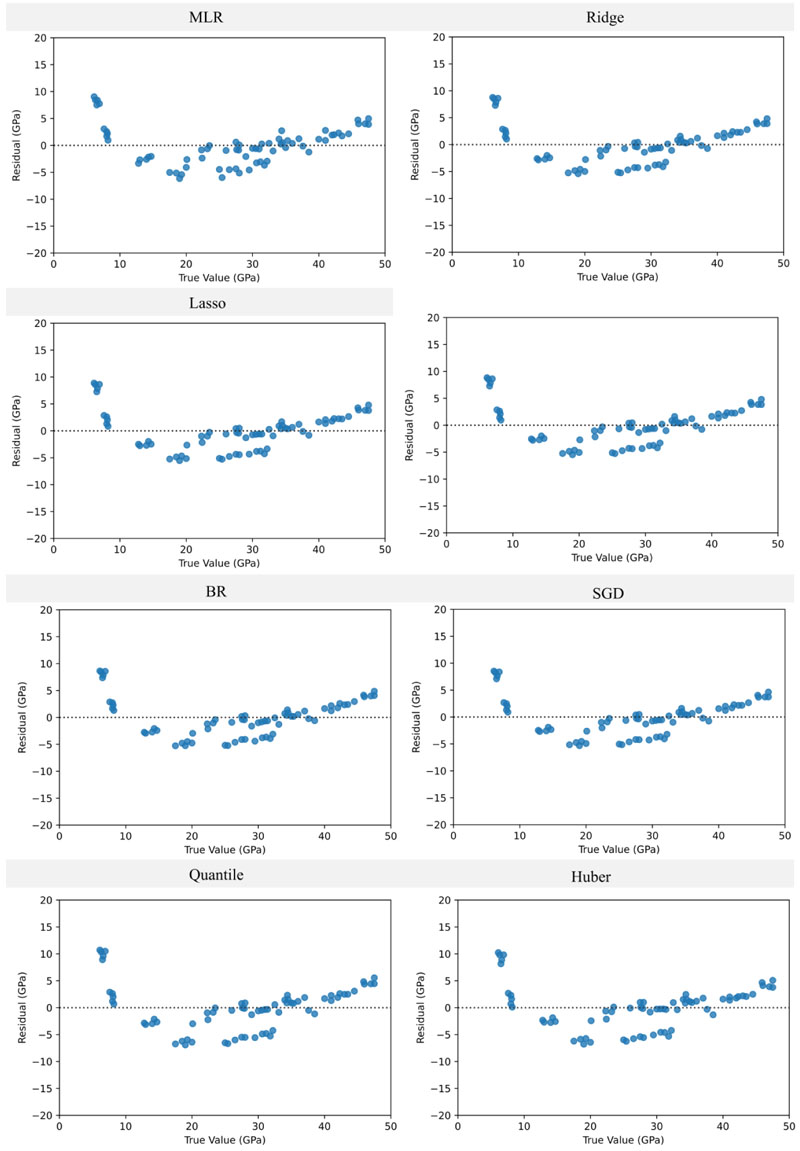
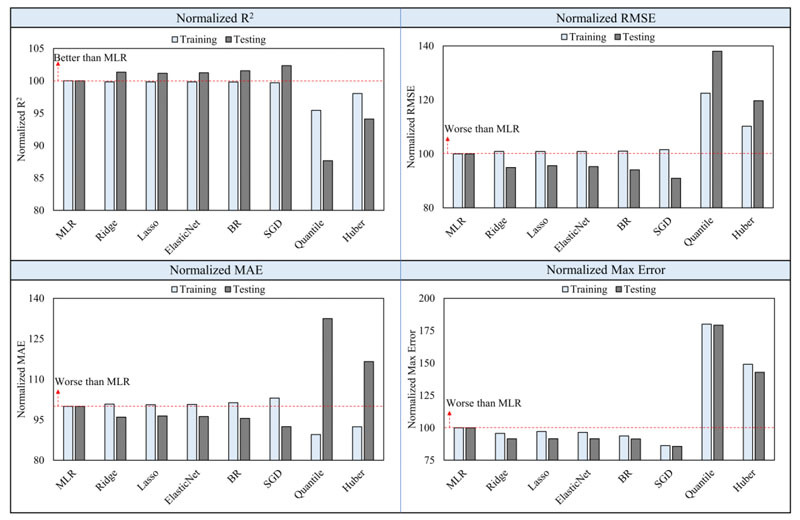
Figs. (9 and 10) show the outcomes of the prediction methods for the modulus of elasticity of RBC mixtures and the models' residual diagrams, respectively. Indeed, the findings show that most models have a comparable performance, which is in line with the observations of the earlier part. Moreover, the fitting rates of the investigated models and their error analyses are indicated in Table 3. Unlike the splitting tensile strength, it can be seen that the maximum coefficient of determination for the testing dataset was 0.9, while the lowest was 0.77, and was measured in the Quantile model. Additionally, it was shown that the best results were obtained using the SGD model, in which its RMSE and MAE were decreased by 9.4% and 7.4%, respectively, compared to the MLR model. In contrast, the performances of the Ridge, Lasso, and ElasticNet were almost identical, and the Quantile had minor outcomes in the training and testing cases. It means that the SGD model is a suitable approach for rapidly estimating the modulus of elasticity of RBC mixtures compared to other techniques.
| Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (GPa) | MAE (GPa) | Max Error (GPa) | R2 | RMSE (GPa) | MAE (GPa) | Max Error (GPa) | |
| MLR | 0.92 | 3.49 | 2.84 | 7.77 | 0.88 | 3.84 | 2.98 | 7.14 |
| Ridge | 0.91 | 3.52 | 2.86 | 7.44 | 0.89 | 3.64 | 2.86 | 6.54 |
| Lasso | 0.92 | 3.52 | 2.85 | 7.54 | 0.89 | 3.67 | 2.88 | 6.54 |
| ElasticNet | 0.92 | 3.52 | 2.86 | 7.49 | 0.89 | 3.66 | 2.87 | 6.54 |
| BR | 0.91 | 3.53 | 2.88 | 7.28 | 0.89 | 3.61 | 2.85 | 6.53 |
| SGD | 0.91 | 3.55 | 2.92 | 6.70 | 0.90 | 3.49 | 2.76 | 6.12 |
| Quantile | 0.87 | 4.28 | 2.54 | 13.99 | 0.77 | 5.30 | 3.95 | 12.81 |
| Huber | 0.90 | 3.85 | 2.62 | 11.58 | 0.83 | 4.59 | 3.48 | 10.21 |
3.4. Comparison of the Regression Analysis Methods
This section is intended to compare and benchmark the performance of the investigated regression models for both the training and testing datasets. The assessment results are shown in Fig. (11) for the compressive strength of RBC, in Fig. (12) for the splitting tensile strength, and in Fig. (13) for the modulus of elasticity of the concrete mixtures. Indeed, it can be seen that for the case of RBC's compressive strength, most models had lower coefficients of determination in the training dataset while achieving higher ones in the testing scenario. This observation is also seen in the cases of the splitting tensile strength and modulus of elasticity of RBC, and can be attributed to the overfitting issues that the MLR model faces while the penalized techniques can control. In addition, the results show that the Ridge, Lasso, ElasticNet, BR, and SGD approaches yield better outcomes compared to the MLR method, with the SGD being the best among them. In contrast, the Quantile and Huber methods have significantly worse behavior than the MLR approach for all of the mechanical properties' estimation cases.

CONCLUSION
This study focused on verifying the capability of various regression techniques to estimate the compressive and splitting tensile strengths and modulus of elasticity of RBC. The results have shown that the MLR model faces some overfitting issues compared to the regularized regression methods, in which the behavior of the MLR model was higher than other approaches in the training case while it was lower in the testing scenario. The investigation results revealed that the SGD is the optimum approach for estimating RBC above properties. Additionally, Ridge, Lasso, ElasticNet, and BR methods performed better than the MLR model, while Quantile and Huber possessed the worst abilities. Finally, it should be mentioned that while artificial intelligence-based technique provides superior accuracy in predicting concrete properties, it raises day-to-day computational problems for practicing engineers. Hence, further research into the capacities and performances of various regression methods in other potential applications is essential and required. Moreover, further investigations in this field are still needed to propose alternative solutions for managing rubber-based solid wastes in the construction industry.
LIST OF ABBREVIATIONS
| RBC | = Rubberized Concrete |
| MLR | = Multiple Linear Regression |
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The authors confirm that the data supporting the findings of this study are available within the article.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


