Measurement of the Hygric Resistance of Concrete Blocks with Perfect Contact Interface: Influence of the Contact Area – Complementary Comments

2.1. Magnitude of the Quantified Post-Interface Flows

It is quite clear that for the determination of the post-interface flows, it is necessary to identify, as good as possible, the knee point in the moisture absorption process, i.e., the moment of interface passing, to quantify the moisture absorption, after that.

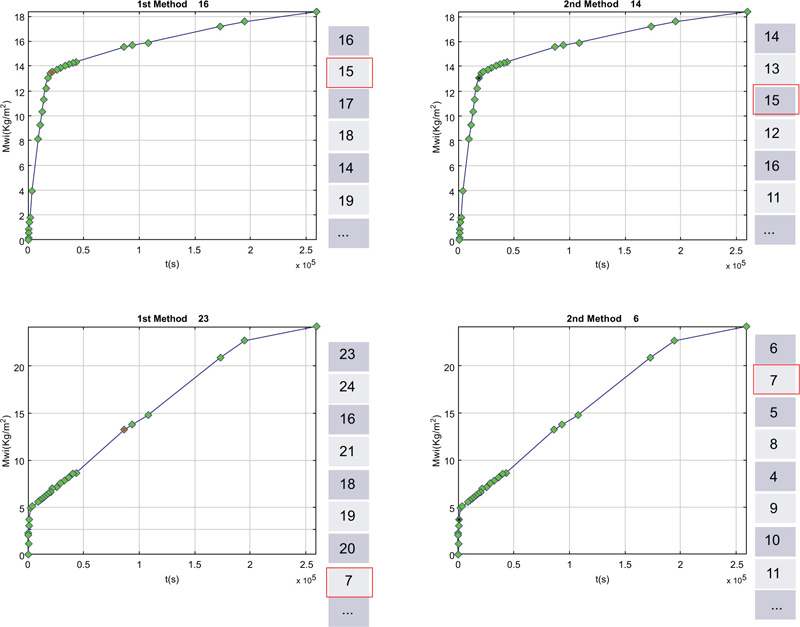
In a paper [8], the hygric resistance was determined by the “knee point” methodology, using the third of the three algorithms [14] and more detailed in Section 2.3. Considering that the hygric resistance should be measured immediately after the first changing point, it was considered important to detect the instant time of the “knee point” using a numerical tool and with better precision as possible. An algorithm based on discrete methods, which was intuitive and easy to implement, was developed by the authors [14] based on literature methods of knee or jump point detection to optimise and overtake some identified limitations.

In a paper [13], the data for the 18 perfect contact moisture absorption curves were digitally extracted [8], and the subsequent knee points were identified using the first method of three algorithms [14], considering the easiest to implement. However, as it will be better explained in Section 2.3, the authors [8] only consider valid the use of the third of the three algorithms. This important difference influences the quantified post-interface flows.

It is clearly explained [13], “for the post-interface flow quantification, at first, the slope of all data points from the knee point onward is calculated, and alternatively, the slope of four data points from the knee point onward…”. Therefore, as a first assumption, the post-interface flow quantification is naturally different when comparing the experimental results [8] and the values extracted digitally.

However, for 2 out of 18 cases, as this option gave a “negative flow”, six data points from the knee point onward were adopted for the slope fitting. As it can be seen, the decision for the number of points to be considered (after the knee) for the post-interface flow quantification was not based on an “independent” methodology. The decision to use 4 or 6 points can change the results of the obtained flow.

The authors [8] do not have a specific methodology (as they proposed for the keen point detection –Section 2.3), so this is a very interesting point to be discussed in the future, i.e., the development of an accurate and independent algorithm to the post-interface flow quantification. Till there, different results can be presented depending on the number of points considered. A scheme of the method adopted for the hygric resistance determination is shown in Fig. (1). This is an interesting topic to be studied deeper, enabling the development of a methodology based on an independent criterion.

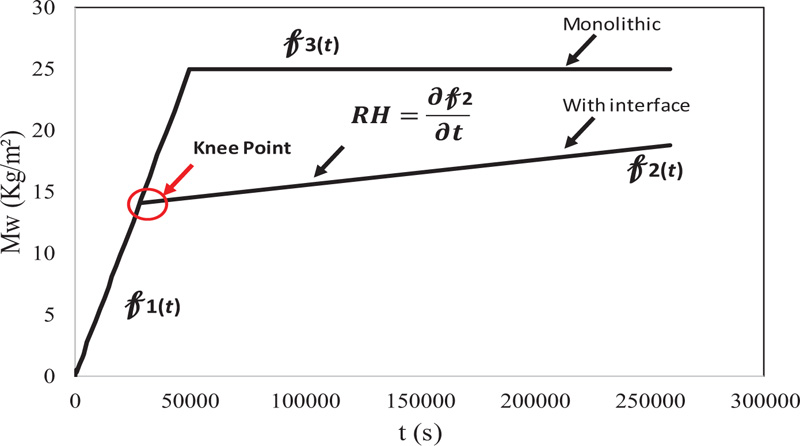
At this stage, the hygric resistance results [8, 13] are different, as the authors consider different methodologies for the knee point detection, and they consider a different number of data points after the knee (different ones) to calculate the slope. A new set of questions that can now be emerged are: Is there a specific number of points to guarantee the “correct” flow? Can a methodology be developed to define which points should be considered? Is this methodology independent of the material, the interface type and position?

However, generalisation of hygric resistance values should be carefully considered. These values are determined specifically for these materials and conditions. The usefulness of the study is more related to the possibility of determining the hygric resistance, when necessary, that could be needed to simulate moisture transport phenomenon than the values themselves Figs. (2 and 3).

2.2. Distinguishability of the Interface Impacts

In a paper [8] the moisture transport in multilayer porous materials by a gravimetric method was analysed, with discontinuities caused by the existence of perfect contact interfaces between the materials at different interface heights. It is well known that these discontinuities cause hygric resistance that retards moisture transport [2, 15-20]. This specific conclusion was not the goal of the paper, as this work aims to understand the effect of the sample cross-section size on the capillary absorption coefficient of concrete samples with and without discontinuities (monolithic samples and samples with perfect contact interfaces at different heights).

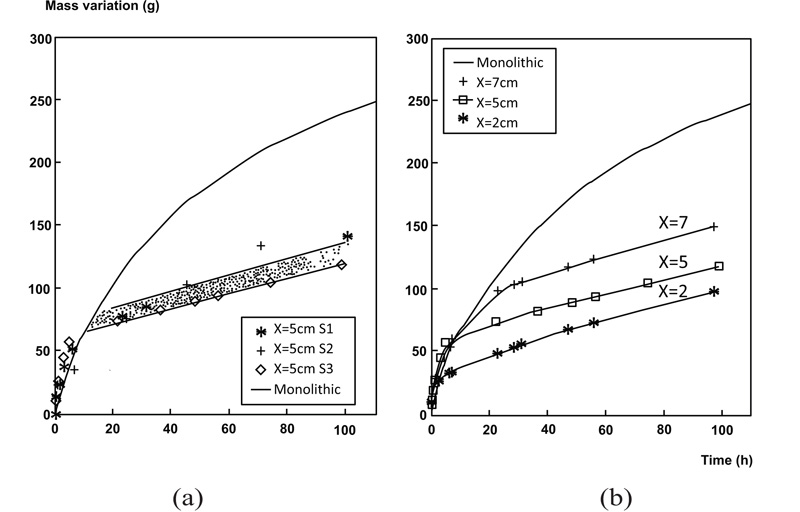
The results presented in Fig. (4) of [8] showed that before the interface, the water absorption of the samples with a perfect contact interface presented similar behaviour as the monolithic samples. However, it is possible to identify a different behaviour when reaching the interface and that change is dependable on the interface position.

It can be said that the hygric resistance (expressed in kg/m²s) is the greater or lesser ease of moisture transfer and is calculated experimentally by the slope of the mass variation curve as a function of time, during a water absorption test, after reaching discontinuity [18, 21, 22]. The “knee point” methodology, using the third of the three algorithms described in a study [8], and more detailed in Section 2.3., was used to determine the hygric resistance values. In a paper [12], the author used data digitally extracted from another study [8] and these data are presented in Fig. (2), “the measured moisture absorption curves for the monolithic of [13] (blue) and perfect contact (orange) samples over the first half-day of the test”. It is considered difficult to identify each class if no colour distinction has been made. However, it is simultaneously said that “the moisture absorption in the perfect contact samples does not reach the highest moisture masses”.

In fact, looking at Fig. (4) of [8] and (Fig. 2) of [13], it is possible to observe and identify a different behaviour when reaching the interface. In the monolithic samples, moisture masses, M_w, reached the highest, and the M_w values became lower when having interface (Fig. 2); similar observations are made in a study [2]. There are some materials where this difference is more evident than other materials.

Additionally, in a paper [13], to further establish the overly similar nature of the moisture absorption in monolithic and perfect contact samples, knee points and quantified post-interface flows were identified for the monolithic samples, a very subjective exercise, given that these samples should not be influenced by an interface. Even considering a strange way of doing it, the most important question is the way of determining the knee points and, consequently, the post-interface flows. It was clearly said [13], “knee points were identified based on the first algorithm of the related paper”, and the authors only consider valid the use of the third of the three algorithms [8].

According to what is explained above, it is possible that the knee-point identification was different, where the authors used a methodology that was validated with many experimental measurements and where they could observe that the first algorithm gives possible incorrect values. This difference has important consequences on the determination of post-interface flows.

2.3. Robustness of the Knee-Point Identification Algorithm

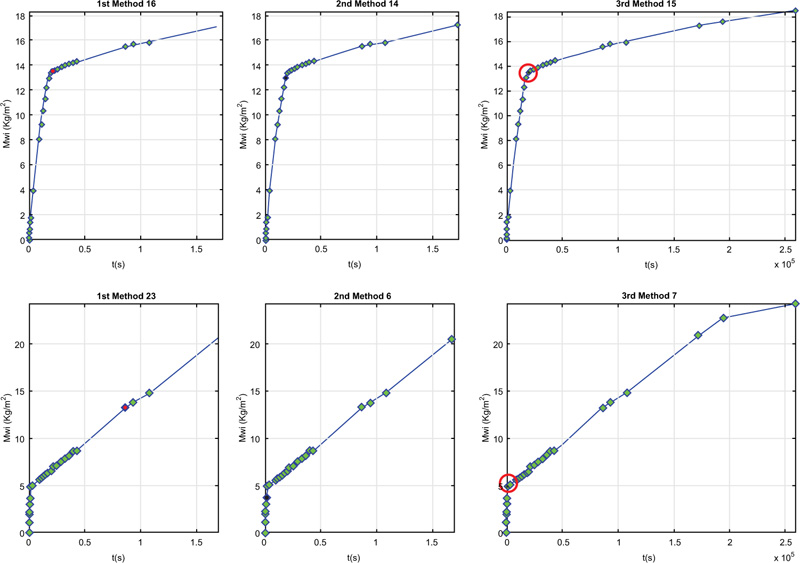
For the knee-point identification, the authors [8] only consider valid the use of the third of the three algorithms [14]. In a study [13], the author applied the first out of three algorithms, considering the easiest to implement, however, this methodology is not considered by the authors [8] as a good solution. In fact, the authors exactly suggest this third methodology (the first two were not developed by the authors but are methodologies proposed in the literature [23-28]) to avoid the limitations identified using those two methods.

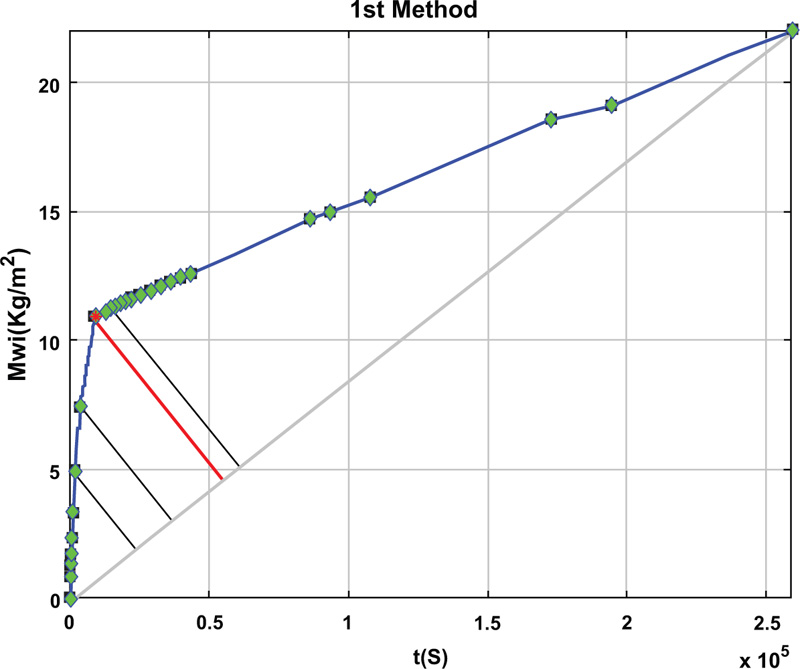
The first method connects the first and last data point with a straight line and identifies the knee point as the point furthest away from that line – (Fig. 3) [13].

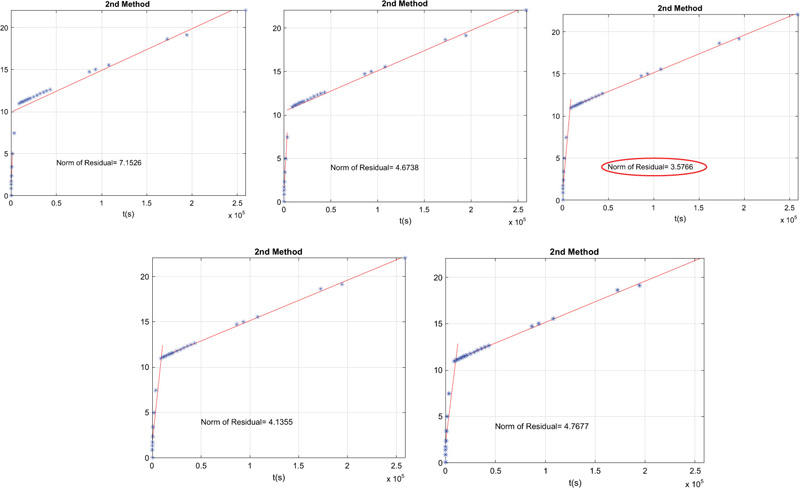
The second method splits the moisture absorption curve into two parts, before and after each measured point and fits separate straight lines to both parts. The point that gives the smallest total deviation between these two lines and the data points is identified as the knee point (Fig. 4). A complete explanation, with examples of knee point detection methods, is presented in previous works [14, 19].

The third method, proposed by the authors, is a combination of the two methods previously presented. The steps of this algorithm are:

(1) Use the 1^st method to calculate, for each point obtained in the measuring procedure, the length of the line segment that is perpendicular to the line that connects the two extreme points of the set. Sort the length of the perpendicular line segment by decreasing order. Let M₁ be the set of indices of the points corresponding to this ordering.

(2) Use the 2^nd method to determine the sum of the errors for the two linear fittings found for each point obtained in the measuring procedure. Sort the sum of the errors for the two linear fittings by ascending order. Designate by M₂ the set of indices of the points associated with this ordering.

(3) Determination of the knee point. Find the point xi = (t_i, M_wi) whose index, i, occupies the best positions in sets M₁ and M₂, using the following algorithm:

Step 0. Let k= 1 be the position of an element in a set, i = 1 an index position and n the total number of points obtained in the measuring procedure.

Step 1. If i > k, let j = 1 and go to Step 3.

Step 2. If M₁(k) = M_2i), the knee point is t(M₁(k)), M_wi(M₁(k)) and stop the algorithm. Otherwise, let i=i + 1 and return to Step 1.

Step 3. If j ≥ k, go to Step 5.

Step 4. If M₂(k) = M₁(j), the knee point is t(M₂(k)), M_wi(M₂(k)) and stop the algorithm. Otherwise, let j = j + 1 and return to Step 3.

Step 5. Let k = k + 1. If k > n, an error message must be sent. Otherwise, let i = 1 and return to Step 1.

Since the main goal of the algorithm proposed is to find the “knee” point of a set of points x_i = (t_i, M_wi), i= 1, 2, …, n obtained in the measuring procedure (discrete points), where the data errors should be considered, the combination of the two previously presented methods can give a “better” knee point. However, as the method is based on discrete points, the data measurements are crucial to guarantee the determination of the best possible point. When proposing the third method, the method was programmed in MATLAB, and the authors did a significant validation of the knee point detection using several data measurements (Fig. 5).

Fig. (6) shows two examples of knee point detection (the same examples presented in Fig. (5), considering the first, the second and the third method, and it is possible to observe that a better solution is obtained with the third method. A complete explanation of knee point detection methods is presented in previous research [14, 19].

The robustness of this knee-point identification using the third algorithm method, which is described in detail [14, 19], could be used in several experimental tests of capillary water absorption existing in the literature with a variety of building materials, from the most common to the most sustainable. In this regard, even though it is not the purpose of this paper, it should not be forgotten that concrete is the most commonly used manufactured building material in the world, however, one of the disadvantages of conventional concrete is its high self-weight and carbon footprint. The manufacturing of 1 ton of ordinary Portland cement is estimated to release approximately 1 ton of carbon dioxide.

Lightweight concrete has low density, reduction of dead load, and increases thermal insulation. There are three types of lightweight aggregate used as a replacement for coarse aggregate: natural lightweight aggregate (as pumice aggregate, volcanic cinder, light sand, etc.), artificial lightweight aggregate (clay ceramisite, expanded perlite, sintered pulverized fuel ash, expanded clay, foamed slag, etc.), and industrial waste lightweight aggregate (as fly ash ceramisite, expanded slag ball, cinder, light sand, etc.). The lightweight aggregate used in this kind of concrete has high porosity, small apparent density, great water absorption, and low strength.

3.1. Capillary Absorption Measurements

This topic discusses the evolution and variation of the moisture absorption for each of the monolithic samples. The presented results [8] were the ones that were experimentally obtained considering the same test methodology, at the same time and in the same conditions. The procedure and the obtained results can be analysed deeper to understand those obtained values.

One explanation could be the material porosity. The authors of a study [8] were not worried about that explanation, and if the authors of another study [13] think that it is important to analyse it deeper, it can be said that this could be verified with independent data. The porosity analysis obtained from vacuum saturation testing, as suggested, was out of the scope of the previous work. The results also showed fast moisture absorption during the first minutes. As was understood [13], one possible reason could be the large pore radii, which could also be verified with independent data, for example, pore volume distributions obtained from mercury intrusion porosimeter (again, this was out of the scope of the previous work).

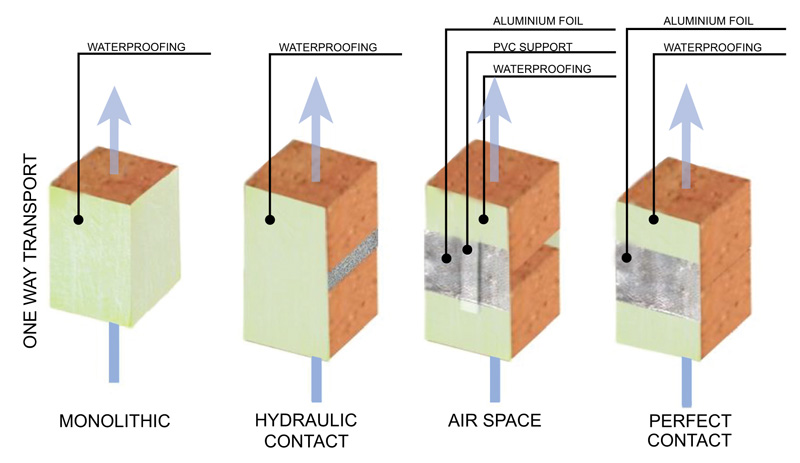
Another issue is the taping quality. The authors have experience with those experimental tests, and when these kinds of tests are made in the Laboratory of Building Physics - LFC, FEUP, Portugal, the “tape” used is an epoxy resin, which is considered a better solution Fig. (7). Taping of the samples was done carefully to avoid additional absorption between the sample and the tape, as the authors are aware [8]. The authors did not try to execute the capillary absorption tests with an incomplete taping, as suggested [13], but this could be made in the future.

3.2. Consistency of the Capillary Absorption Processing

The authors [8] studied the capillary absorption of monolithic samples, in which the impact of the sample cross-section size is the main aspect. The capillary absorption tests on 15 cm height monolithic concrete samples, with cross-sections of 5x5 cm², 7.5x7.5 cm², 10x10 cm², were made, and those results are shown in Fig. (3) of paper [8] (not in Fig. (3) of paper [13]). It is said that “data in that figure have been digitally extracted” and all the discussions after that, with precise numbers and deviations, were based on that “approximation” [13].

It seems to the authors that this procedure should be a way to obtain reasonable compared results but not the same as it is not possible to have that precision (especially in the first overlapped density of points). So, it is considered expectable some deviations between the C [g/cm²] and A_w [kg/m²s^0.5] [8] and the Moisture Mass (3 days) [g/cm²] average and Moisture Mass (1 day) [kg/m²] average [13].

Apart from the expected deviation considering the digitally extracted method [13, 8], it is said that “The Brazilian standard NBR 9779 establishes only the “C” calculation (in g/cm²), called capillarity absorption, presented in Table 4, made for all monolithic specimens”. This means that all the samples were considered in the C calculations. Nevertheless, as it is also said, “The 3 more representative experimental results for each contact area are represented in Fig. (4)”. This does not influence the conclusions/finding of the article [8].

In fact, looking at Table 2 of [13], the only deviation that feels strange is the A_w of the sample with 10x10 cm² of a cross-section. After a deep analysis of the entire study done [8], it was observed that the correct value (for the A_w of the sample with 10x10 cm² of cross-section) should be 0.1013 kg/m²s^0.5 (the value of a discarded sample was used instead of the presented samples). However, it should be highlighted that this does not influence the conclusions/finding of the article.