Design and Analysis of Automated Rack Supported Warehouses

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Design and Analysis of Automated Rack Supported Warehouses

Silvia Caprili, * Open Modal Francesco Morelli Walter Salvatore Agnese Natali
Authors Info & Affiliations
The Open Civil Engineering Journal • 29 Jun 2018 • RESEARCH ARTICLE • DOI: 10.2174/1874149501812010150

Abstract

Background:

The lack of codified standards for the design of automated rack supported warehouses forced engineers to use personal experience and commonly accepted rules.

Objective:

This paper investigates the efficacy of applying Eurocodes’ rules for the design and analysis of automated rack supported warehouses. Structural performance, construction feasibility and economic effort are considered.

Method:

A typical case study building was designed following the two approaches proposed by Eurocodes: elastic and dissipative.

Results:

The satisfaction of the capacity design requirements, used for dissipative approach, was not always possible. Analyses showed the development of non-uniform collapse mechanisms and yielding patterns.

Conclusion:

Specific design rules and analysis techniques shall be developed accounting for the structural performance of automated rack supported warehouses.

Keywords: Warehouses, Seismic design, Steel structure, Capacity design, Industrial building, Storage constructions.

1. INTRODUCTION: STEEL RACKS AND AUTOMATED SUPPORTED RACK WAREHOUSES

Storage warehouses constructions have the main function of storing goods after production and before market distribution. Different typologies of storage warehouses developed in the past decades; their geometrical and structural characteristics varied due to producers’ needs and practical experience, without following codified standards or design methodologies.

A basic distinction exists between traditional Steel Racks (SR) and Automated Rack Supported Warehouses (ARSW). SR are designed to carry on the structural self-weight and the weight of the stored goods. ARSW are self-bearing rack structures devoted to support, besides self-weight and weight of products, environmental loads (i.e. wind, snow and seismic action) and all the other non-structural elements such as clads, roof, technological facilities, equipment, etc.

If indications help the design of SR, no provisions currently exist for ARSW: designers follow companies’ requirements and practical experience, sometimes supported by experimental evidence. Plenty of researches were conducted during last years concerning SR, but only several works dealt with ARSW, mainly related to logistic aspects without analysing structural issues.

Storage warehouses, both SR and ARSW, present different plan layouts to optimize the costs due to material storage and handling, as function of the logistic needs. Boysen et al. [1], De Koster et al. [2] and Cardona et al. [3] deeply analysed the picking order sequences used in warehouses, highlighting their dependence on typology of goods, market organization, openings’ distribution, period of the year, etc.

The traditional structural scheme of steel SR consists of a regular sequence of upright frames connected by coupled pallet beams devoted to carry on the goods, as widely presented by Bernuzzi [4]. The bracing system is forced in the transversal direction to maximize the storage capacity. Structural elements frequently adopt cold formed profiles with non-bisymmetric cross-section; this solution optimizes the structural performance by reducing the steel weight and the costs due to the skeleton frame [5]. Slenderness and buckling aspects, as well as realization of joints and connections, shall otherwise be accounted for.

In the past, only vertical gravitational loads (self-weight and stored goods) ruled the design of SR. The adopted safety levels towards vertical and horizontal actions were assessed in relation to producers’ needs, not respecting prescriptions imposed for steel constructions. Recent experimental and numerical investigations performed by Kanyilmaz et al. [6, 7] showed the unexpected seismic performance of SR, characterized by sudden and brittle failures, especially if compared to ordinary steel constructions. It was shown that several factors handle this situation, which are the presence of perforations in the thin wall of the uprights, the typology of connections between elements and the employment of cold-formed profiles instead of hot-rolled ones [8]. Based on these considerations and on the results of experimental campaigns on real scale prototypes performed in two successful European projects (Steelrack [9] and Steelrack 2 [10]), guidelines and indications for the seismic design of SR developed. Currently, EN16681:2016 [11] allows the safe and reliable design of traditional pallet steel racks.

If recent specific design rules exist for SR, no prescriptions raise about ARSW. ARSW are complex steel constructions provided by sophisticated automated machines for the handling of products. ARSW developed in the last decade based on the need for bigger and optimized working spaces, able to increase the market, thanks to the continuous development of the storage technology.

ARSW can be more than 100 m long and 30 m high; the racks, extending to the full height of the building, represent the load-bearing structure. Racks present a high number of reduced-height inter-storey (1.0÷1.30 m) and two consecutive lanes of racks with usually 2.0-2.5 m large loading-unloading isles, where machines are located.

The geometrical characteristics of ARSW and the automated handling of pallets allow the full exploitation of the available space. Statistical analyses highlighted that the pallets, in fully load conditions, cover about the 54% of the plan surface and the 40% of the volume. In serviceability condition, not all the shelves are full: the distribution of pallets depends on logistic strategies, ruled by picking order sequences like the ones adopted for SR. The products’ organization affects the behaviour of ARSW during seismic events, being responsible for masses’ distribution. Nowadays, the design of ARSW follows companies’ needs with a practical based-experience approach. This situation exposed structures to relevant damages in case of seismic events, as highlighted during the last 2012 Emilia-Romagna earthquake. It was the case, for instance, of Ceramiche Sant’ Agostino storage warehouse [12, 13, 14]. Being ARSW not designed to support seismic action, total or partial collapses in case of earthquake event are frequent, causing problems not only from the life-safety point of view but also considering financial aspects. The interruption of production and activities leads to relevant economic losses and efforts to recover the pre-emergency condition.

The need for safe and reliable design guidelines for ARSW becomes then clear. Since ARSW strongly differ from SR in terms of loading conditions and geometry, EN16681:2016 [11] cannot be used. One possibility is the application of Eurocodes 3 and 8 requirements for steel constructions, even if differences exist also in this case: it is enough to think to the number of storeys with reduced height and to their geometrical configuration. The interest on the topic is well evidenced by the financing of the European research project “STEELWAR: Advanced structural solutions for automated STEEL rack supported WARehouses”, Research Fund for Coal and Steel grant agreement N. 754102, 2017-2021.

Stating the above considerations, this paper investigates the efficiency of Eurocodes’ design and analysis rules for ARSW, in terms of feasibility, structural performance and costs to determine the eventual need of further studies and applications.

Advantages and disadvantages, structural performance and feasibility of proposed solutions are evaluated and deeply discussed.

2. METHODOLOGY

An ARSW case study building was designed following European standards [15, 16]. Loading indications coming from Italian National Standards for Constructions [14] were considered. Two approaches (elastic – EA and dissipative – DA) were adopted for the design, highlighting differences in terms of steel weight, seismic performance at Life Safety (LS) limit state, collapse mechanisms, construction details and other relevant aspects.

The Elastic Approach (EA) pursued the realization of buildings provided by a non-dissipative behaviour according to Eurocode 3 for steel structures. Structural members should remain in the elastic field without the development of dissipative mechanisms. Elastic seismic action (unitary behaviour factor) was used.

The Dissipative Approach (DA) pursued the realization of structures following the capacity design approach of Eurocode 8 [15]. The respect of specific details’ indications for joints and connections and for the determination of design actions of protected members was mandatory. Elastic response spectrum was reduced by the application of a behaviour factor higher than 1.0.

Numerical nonlinear models and analyses allowed to investigate the structural performance of ARSW buildings. Several problems concerning the efficacy of the capacity design approach, when applied to ARSW, were highlighted. Analyses’ results showed the need of a revised design approach for ARSW to assure the desired structural performances, adequate safety and easiness during the assembly phase. Fig. (1) summarizes the method adopted in the manuscript.

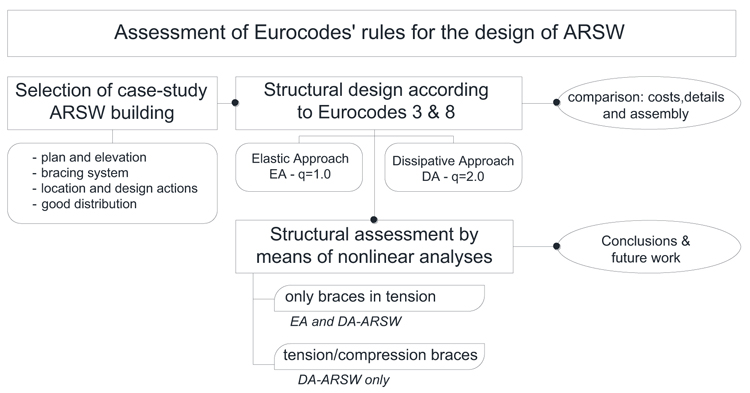
Fig. (1). Scheme of the methodology adopted in the paper.

3. DESIGN OF ARSW STRUCTURES

3.1. Selection of the Case Study

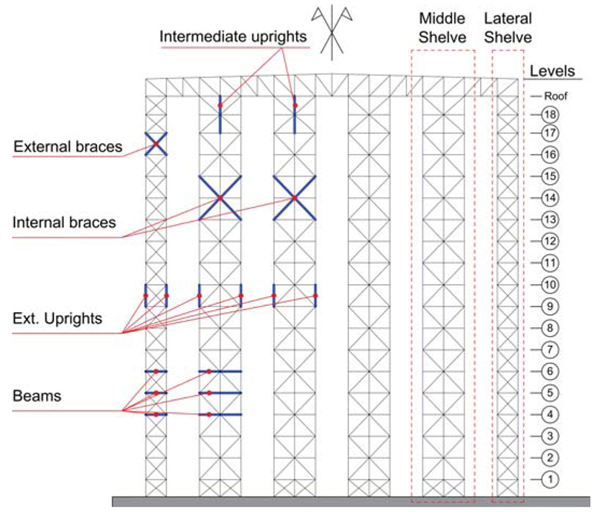
The selected case study is a 24.47 m high rectangular plan building (21.5x74.8 m) with X-shaped concentric braces configuration. The case study is representative of Italian ARSW of the last decades. 10 lines of racks – two on the sides and the others coupled in the middle – with a total of 19 storeys with a maximum inter-storey height equal to 1.30 m, 17 loading levels and 5 loading-unloading aisles were present. The weight of each pallet weight was 1000 kg, resulting in a whole global warehouse capacity up to 12.580 pallets. The general organization of the building is presented in Fig. (2).

Fig. (2). Transversal and longitudinal sections of the ARSW case-study building. A generic distribution of pallet is also presented.

3.1.1. Design Criteria and Assumptions

Profiles with sections belonging to Class types 1, 2 or 3 were adopted [15-17]. Profiles with sections of Class 4 were used only for the longitudinal beams carrying on the pallets. In case of DA, other profiles replaced angular sections to guarantee the correct dissipative behaviour.

To compare the two design strategies, for the same structural elements, the same section profiles were adopted, modifying the thickness and the steel grade in relation to the design demand and the need to satisfy Eurocodes’ prescriptions.

Table 1.
Definition of the design loads.
Dead Load – G1 According to the Steel Profiles Used.
Permanent/non-structural loads G2 Roof panels: 0,20 kN/m2
Side panels: 0,25 kN/m2
Accidental loads Qk Stored goods: each pallet is 1000 kg. The weight of each pallet is reduced by 15% basing on current practice.
Live load on roof: 0.50 kN/m2
Wind action 1.15 kN/m2 for the upwind side 0.69 kN/m2 for the downwind side
Snow load: 1.2 kN/m2
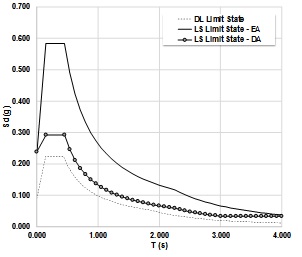
Definition of the Seismic action for the design (§ 3.2.3 of NTC2008)
Soil of category C.		 DL limit state LS limit state (EA) LS limit state (DA)
ag 0.06 g 0.163 g 0.163 g
F0 2.507 2.449 2.449
Tc* 0.269 s 0.284 g 0.284 g
q 1.00 1.00 2.00

The uprights presented rectangular hollow sections (class 1), the beams adopted double channel sections (Class 1) and for the bracing system, angular (Class 3 – in case of EA) and rectangular hollow sections (Class 1 - in the case of DA) were selected. C-shaped cold formed profiles were used for the longitudinal beams carrying the pallets.

3.1.2. Design Loads and Combinations

The design loads were defined in relation to the building site (Modena, Italy); Table 1 summarizes adopted actions.

Linear dynamic analyses with response spectra were performed. Behaviour factors (q) were respectively equal to 1.0 and 2.0 for EA and DA. Technical reasons justify q=2.0: for example, the need of achieving Damage Limitation (DL) actions lower with respect to Life Safety (LS) ones, adoption of medium/low ductility class to simplify connections, satisfaction of Eurocodes’ requirements etc. The pallets’ weight was evaluated referring to the full load condition neglecting the influence of the load distribution. The weight of each pallet was reduced by 15%: this last assumption, not exactly representative of the current condition of ARSW, maximized the seismic masses.

3.2. Design with Elastic Approach (EA)

The design was executed performing a linear dynamic analysis with unitary response spectrum. The structural scheme adopted (X-braces in tension) neglected the contribution of braces in compression.

The three-dimensional model of the structure was realized using SAP2000® software (Fig. 3). All the steel members (uprights, beams, braces) were modelled as mono-dimensional frame elements. Connections were designed and modelled as pinned joints, except for the column-to-foundation connection, fixed in both directions.

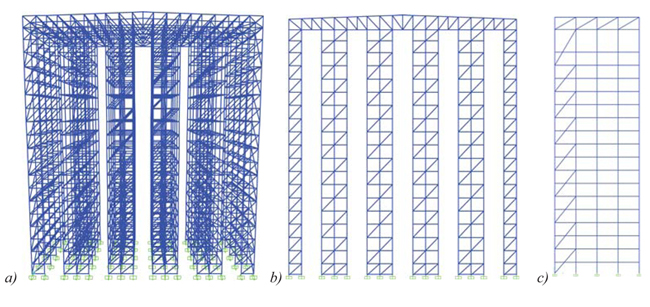
Fig. (3). Three-dimensional model for the designed ARSW building: a) global view; b) transversal view; c) longitudinal view.

Structural elements and connections were designed to elastically resist the design actions [16]. The deformability of the structure was checked against DL limit state, keeping the maximum inter-storey drift lower than the imposed limitation.

Three different sections were adopted for vertical braces: L45x45x5, L50x50x5 and L60x60x5, steel grade S355.

Modifications of elements’ section along the whole height of the frame were applied, resulting in several different construction details (Table 2).

Table 2.
Summary of profiles and materials adopted for the different structural elements considering EA and DA.
ARSW Designed with EA - Transversal Frame ARSW Designed with DA - Transversal Frame
Element Section & material Element Section & material
Roof Truss Roof Truss
Struts and ties Double Angular Section 45x45x4 S355 Struts and ties Double Angular Section 45x45x4 S355
Diagonals Double Angular Section 55x55x4 S355 Diagonals Double Angular Section 55x55x4 S355
External Uprights External Uprights
9th level- roof Rectangular Hollow Section 120x80x4 S355 9th – roof levels Rectangular Hollow Section 120x80x4 S355
5th -8th levels Rectangular Hollow Section 120x80x8 S355 5th - 8th levels Rectangular Hollow Section 120x80x6 S355
1st - 4th levels Rectangular Hollow Section 120x80x10 S355 1st - 4th levels Rectangular Hollow Section 120x80x10 S355
Intermediate Uprights Intermediate Uprights
9th level/roof Rectangular Hollow Section 150x100x6 S355 9th – roof levels Rectangular Hollow Section 150x100x4 S355
5th - 8th levels Rectangular Hollow Section 150x100x8 S355 5th - 8th levels Rectangular Hollow Section 150x100x6 S355
1st - 4th levels Rectangular Hollow Section 150x100x10 S355 1st - 4th levels Rectangular Hollow Section 150x100x10 S355
Beams Beams
All Beams Double Channel Section 80x50x3 S355 All beams Double Channel Section 80x50x3 S355
Bracing elements Bracing elements - External braces
11th level/roof Angular Section 45x45x5 S355 15th – roof levels Angular Section 30x30x4 S235
7th - 10th level Angular Section 50x50x5 S355 11th -14th levels Angular Section 35x35x4 S235
1st - 6th levels Angular Section 60x60x5 S355 10th level Angular Section 35x35x4 S275
4th - 9th levels Angular Section 40x40x4 S275
1st - 3rd levels Angular Section 40x40x5 S355
Internal braces
15th – roof levels Rectangular Hollow Section 30x30x2 S235
12th -14th levels Rectangular Hollow Section 30x30x2.5 S235
7th - 11th levels Rectangular Hollow Section 30x30x2.5 S275
2nd - 6th levels Rectangular Hollow Section 30x30x2.5 S355
1st level Angular Section 40x40x4 S355

Connections were welded in the transversal direction to give continuity among the uprights and to fix the other elements on them through a supporting steel plate. In the longitudinal direction, the beams bearing the pallets were bolted to supporting brackets welded to the transversal beams.

3.3. Design with Dissipative Approach (DA)

The capacity design philosophy was followed to develop a global ductile collapse mechanism through the localization of plastic deformations in correspondence of braces in tension. The modelling approach, environmental and live loads were the same assumed for the EA; seismic action adopted a behaviour factor equal to 2.0.

The contribution of compressed braces was, as well, not considered in agreement to Eurocode 8 [15]. In the case of X-braces steel structures, the development of plastic hinges in braces shall precede bucking phenomena in compressed members and the failure of the connections in the dissipative zones. All the other elements (uprights, beams) remain elastic being over-strengthened respect to braces.

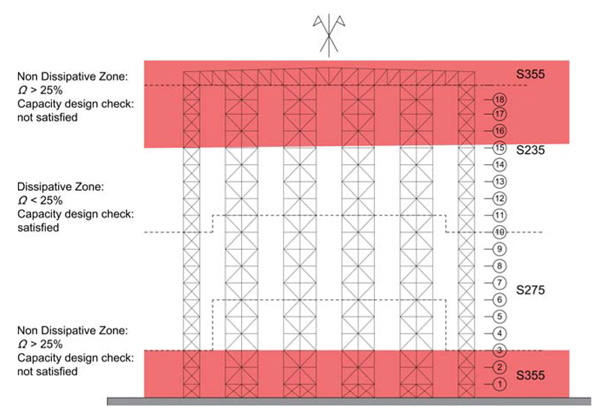
The adoption of cross-section profiles of Classes 1 or 2 for the dissipative elements and the satisfaction of specific limitations for the non-dimensional slenderness ratio (1.3 ≤λ≤2.0) are mandatory for DA. Besides, the maximum allowed variation along the height for the over-strength factor Ω, defined as the ratio between the tensile force resistance (NPl,Rd,i) and the design tensile force (NEd,i) of the i-th dissipative element (Eq. 1), is imposed up to 25% (Eq. 2). This prescription guarantees the development of a global yielding pattern.

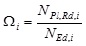(1)

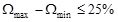(2)

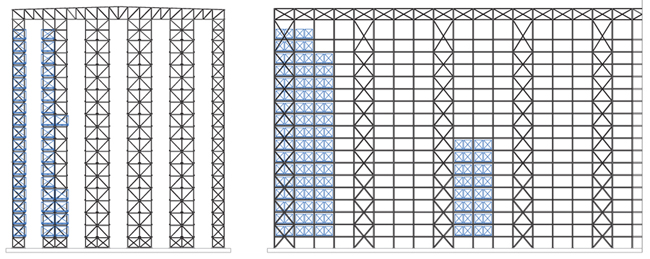
Due to the reduced inter-storey height and the high number of storeys, the satisfaction of the capacity design requirements was not easy. A wide variation of profiles’ sections and materials allowed to respect the slenderness limits imposed. The satisfaction of the Ω restriction was, otherwise, not always possible, resulting in two non-dissipative zones in correspondence of the top and of the bottom of the construction. Table 2 summarizes the profiles and the corresponding materials adopted for the different structural elements following EA and DA; the identification and the numbering of levels are defined according to Fig. (4). Fig. (5) shows the portions of the ARSW where Eurocodes’ prescriptions for dissipative structures are not respected, providing indications concerning the different steel grades adopted. The same typologies of connections (bolted, welded) used for EA-ARSW, were adopted for DA-ARSW. A wide variety of construction details, resulting in higher difficulties during construction phase and higher construction costs with respect to the EA solution, was obtained. Table 3 summarizes the profiles and the corresponding materials adopted for the different structural elements following the DA.

Fig. (4). Numbering of the different levels/storeys and indication of typical components in ARSW.
Fig. (5). Dissipative structure, transversal frame: non-dissipative zones and adopted steel grades.

3.4. Comparison between Elastic and Dissipative Approaches

The comparison between the structural solutions achieved with EA and DA highlight positive and negative aspects, mainly concerning the total weight of the structures (i.e. material cost) and the typology of joints and connections (i.e. manpower and construction costs).

The weight of each transversal frame was equal to 10,47 tons and 9,28 tons in the case of, respectively, EA and DA.

The resulting base shear forces acting at LS were respectively equal to 435 kN and 197 kN for EA and DA, because of the different design seismic action and, besides, seismic masses of the two buildings.

Since no specific capacity design rules are prescribed for structural details, connections are easier in EA-ARSW if compared to structural details required for DA-building. Differences in sections and materials resulted in a wide range of construction details and to the increase of construction costs. Table 3 summarizes the differences between EA and DA solutions for the design of ARSW structures.

Table 3.
Summarizing table of pros and cons of dissipative and non-dissipative approach for ARSW design.
Elastic Approach for design (q=1.0) Dissipative Approach for design (q=2.0)
Pros Easier prescription to be respected Lighter structure (9.28 tons)
Easier construction details
Cons Heavier structure (10,47 tons) Complexity for the variety of construction details
Higher actions and requested resistance Not full satisfaction of capacity design requirements

4. STRUCTURAL ASSESSMENT OF ARWS: RESULTS AND DISCUSSION

Nonlinear static analyses were carried out on bi-dimensional plane frames representing the typical transversal section of the case study building. Analyses were performed using SAP2000® in two following steps: in the first step only braces in tension were considered; the second step also included the contribution of compressed braces, using opportune modelling techniques. A lumped plasticity approach was adopted for numerical simulations.

4.1. Analysis Including only Braces in Tension

4.1.1. Modelling of Braces in Tension

Plastic hinges were located in braces in tension, dissipative members in the structural scheme adopted. A zero-compression limit was applied to each brace to neglect its contribution when compressed.

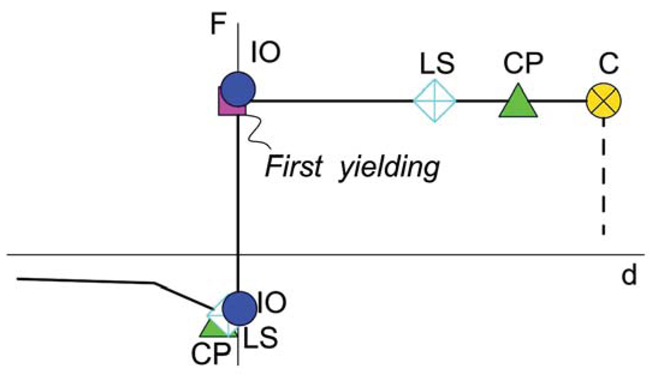
An elastic perfectly plastic behaviour characterized plastic hinges. Fig. (6) shows the adopted force/displacement relationship; different colours and symbols are associated to the achievement of different Limit States (immediate occupancy – IO, life safety – LS and collapse prevention – CP). The model of the plastic hinge included also the first yielding (represented by a magenta square) and a point beyond CP introduced to solve convergence problems (represented by a yellow crossed circle). The degrading branch, needed by the software, was not relevant for the analysis. The acceptance criteria for each limit state are provided by EN1998-3:2005 [18], being Δt the elongation of the considered element, hereafter summarized.

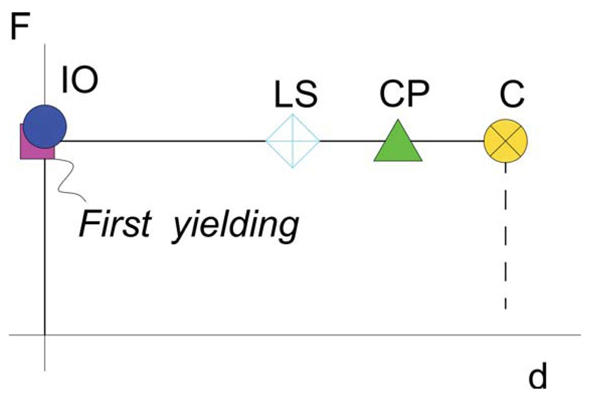
Fig. (6). Force/displacement diagram adopted for plastic hinges in tense braces.
  • Limit for Immediate Occupancy - IO (blue circle): 0,25·Δt.
  • Limit for Life Safety - LS (light blue rhombus): 7,0·Δt.
  • Limit for Collapse Prevention - CP (green triangle): 9,0·Δt.

4.1.2. Nonlinear Static Analysis: Results

Pushover analysis adopted two different load distributions: the 1st group is characterized by incremental horizontal actions proportional to the shear forces at each level of the ARSW; the 2nd group is characterized by incremental horizontal forces proportional to the masses.

Analyses were performed in displacement control; positive force is directed from left to right. Results are presented in terms of capacity curves: the control point was fixed in correspondence of the top storey of the structure.

For each dissipative element, the achievement of the different limit states of Fig. (6) was assessed. In the case of DA-ARSW, forces acting on non-dissipative members were checked to confirm the efficiency of the capacity design.

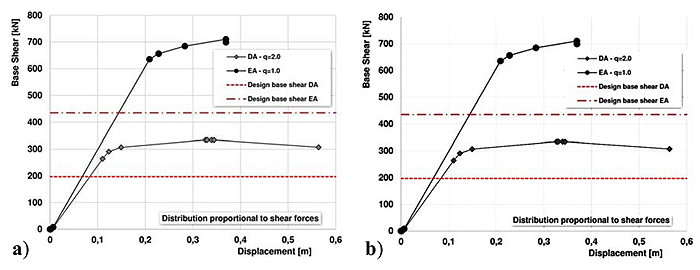
Fig. (7) shows the capacity curve obtained for EA-ARSW using the 1st group distribution and the yielding pattern achieved at collapse limit state. As visible, considering the seismic design base shear (435 kN), the structure was still in the elastic field. The collapse condition was achieved in correspondence of several braces in the bottom part of the building for a displacement equal to about 37 cm and base shear equal to 710 kN.

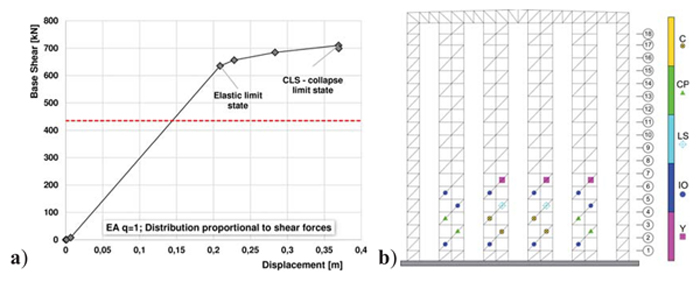
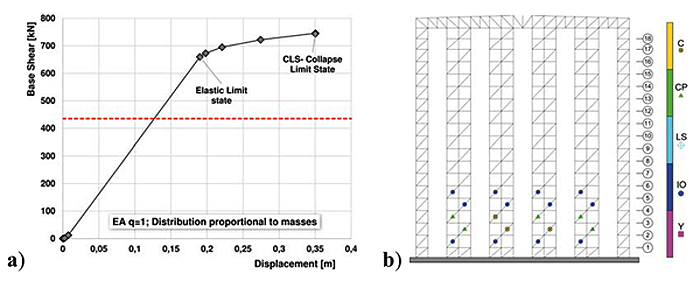
Fig. (7). a) Capacity curve of ARSW designed for q=1.0 for 1st group distribution; b) yielding pattern and achievement of different limit states in correspondence of the last step of the analysis (about 37 cm of displacement).

Fig. (8) shows the capacity curve obtained for EA-ARSW using the 2nd group distribution and the yielding pattern achieved at collapse limit state. In this case also, considering the seismic design base shear (435 kN), the structure was still in the elastic field. The collapse condition was achieved in correspondence of several braces in the bottom part of the building for a displacement equal to about 35 cm and base shear equal to 745 kN.

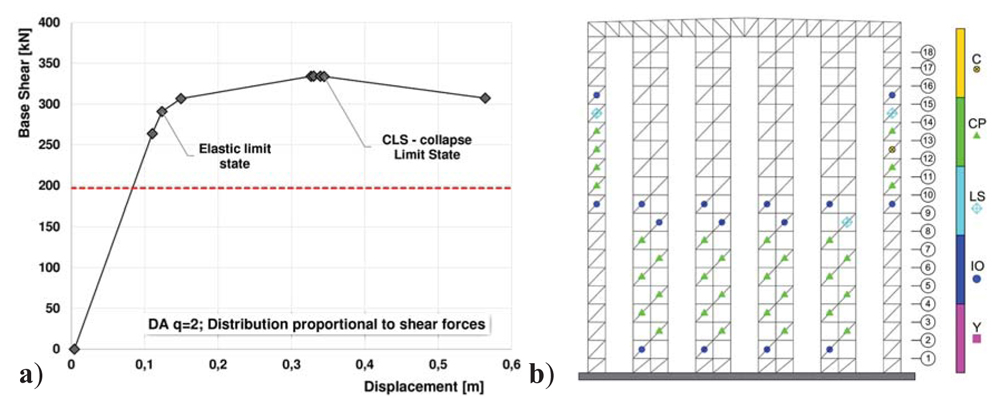
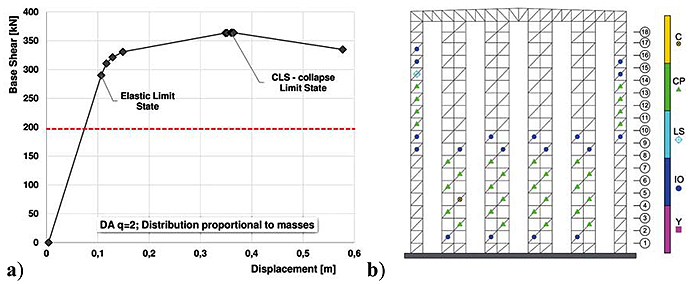
Fig. (8). a) Capacity curve of ARSW designed for q=1.0 for 2nd group distribution; b) yielding pattern and achievement of different limit states in correspondence of the last step of the analysis (about 35 cm of displacement).

Similar considerations are valid in the case of pushover analysis on DA-ARSW. Figs. (9 and 10) highlight, once again, that for a base shear equal to the design one (about 197 kN) the structure exhibited an elastic behaviour. The collapse condition – achieved for values of displacements and base shear respectively equal to 34 cm and 333 kN for 1st group forces and to 35 cm and 363 kN for 2nd group forces – corresponded to a wider distribution of plastic hinges, in correspondence of the central bottom part of the building and, in parallel, of the external uprights.

Fig. (9). a) Capacity curve of ARSW designed for q=2.0 for 1st group distribution; b) yielding pattern and achievement of different limit states in correspondence of the last step of the analysis (about 33 cm of displacement).
Fig. (10). a) Capacity curve of ARSW designed for q=2.0 for 1st group distribution; b) yielding pattern and achievement of different limit states in correspondence of the last step of the analysis (about 33 cm of displacement).

Comparing EA and DA-ARSW structures, relevant differences in the yielding pattern developed were observed (Fig. 7 ÷ Fig. 10). In EA-ARSW plastic hinges mainly developed in the central bottom part of the frame; in the case of DA-ARSW also lateral braces were involved in the developed mechanism.

Table 4 presents the values of base shear and displacement at yielding and collapse; in the table, ELS and CLS are acronyms used, respectively, to show the elastic and the collapse limit states.

Table 4.
Base shear and displacement values corresponding to yielding and collapse for ARSW case study buildings.
Pushover Analyses EA (q=1.0) 1st Group EA (q=1.0) 2nd Group DA (q=2.0) 1st Group DA (q=2.0) 2nd Group
ELS CLS ELS CLS ELS CLS ELS CLS
Base Force [kN] 635 710 660 745 291 333 290 363
Displacement [cm] 21 37 19 3 12 34 11 35

Looking at Fig. (11), for the same displacement of about 120 mm (i.e. value indicating the end of the elastic behaviour of the DA-ARSW), the EA structure was in the elastic field, while the first plastic hinges developed in the lower bracing elements of the dissipative structure. It is otherwise to be noted that for the EA-ARSW, the capacity curve beyond the elastic limit is provided by a mechanical relevance only if the connections among elements are enough over-resistant respect to the bracings. This condition, currently, is not mandatory for non-dissipative structures [15-17].

Fig. (11). Comparison of the capacity curves obtained from the EA and DA-ARSW: a) 1st distribution of horizontal forces; b) 2nd distribution of horizontal forces.

Referring to the yielding patterns, the DA allowed a major diffusion of plastic hinges: the higher parts of the external lines of racks took part to the mechanism. Although a wider distribution of plastic hinges was reached, a global collapse mechanism was not achieved.

4.2. Analysis Including Braces in Compression

4.2.1. Modelling of Braces in Compression

Further analyses were performed including the contribution of compressed braced for the DA-ARSW. An asymmetric tension/compression behaviour characterized each plastic hinge: for the tensile force/displacement relationship, the same limitations presented for only-tension braces were adopted. The compressive behaviour was calibrated basing on preliminary numerical simulation on single brace elements.

A simple fibre model was realized using OpenSees® [19] following methods widely presented in the current scientific literature [20, 21, 22]. An initial imperfection, equal to 1/500 of the total length of the element, was applied to model bucking phenomena; a constitutive elastic-perfectly plastic law was adopted for the material. Pushover analysis were performed to simulate the behaviour of compressed members (Fig. 12); results in terms of displacement/base shear are presented for two different sections, according to what presented in Badalassi et al [12].

The equivalent quadri-linear force/displacement law was extracted basing on energy equivalence considerations: the continuous curve was obtained from nonlinear analyses on the fibre compressed element, the dashed one represents the approximation to use in the model.

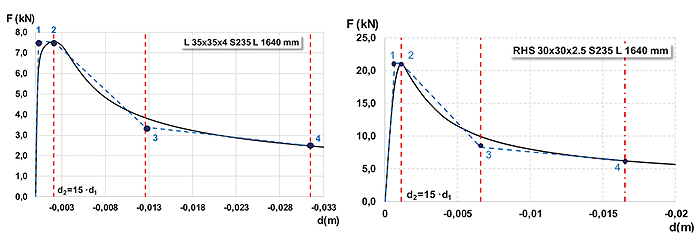
Fig. (12). Determination of the equivalent quadri-linear relationships for: a) angular L35x35x4 profile, length 1640 mm steel grade S235; b) rectangular hollow section 30x30x2,5, length 1640 mm, steel grade S235.

The quadri-linear force/displacement law is defined as follows:

  • The first branch (O-1) is a parallel to the almost linear part of the curve till the greatest force is reached.
  • The second branch (1-2) is the horizontal segment till point 2 is reached (point 2 is the point of the original curve where the maximum force is reached).
  • Point 4 is the point of the original curve corresponding to d2=15·d1, being d1 the displacement at point 1.
  • Point 3 is defined basing on the energy equivalence considerations between the two curves.

Fig. (13) shows the force/displacement relationship adopted for each plastic hinge. The different colours correspond to the different limit states. The acceptance criteria are provided by EN1998-3:2005 [18], being Δc the shortening of the considered element.

Fig. (13). Force/displacement law adopted for each plastic hinge.
  • Limit for IO (blue circle): 0,25·Δc for profiles of class 1 and 2.
  • Limit for LS (light blue rhombus): 4, 0·Δc for profiles of class 1 and 1,0·Δc for profiles of class 2.
  • Limit for CP (green triangle): 6,0·Δc for profiles of class 1 and 1,00·Δc for profiles of class 2.

4.2.2. Nonlinear Static Analysis: Results

The lumped plasticity bi-dimensional model of DA-ARSW was developed with SAP2000®; the model included braces in both tension and compression. Pushover analyses were performed using the same forces distribution described in the previous paragraph. Fig. (14) shows the capacity curve for the 1st distribution of forces. Points A, B, C and D refer to the relevant conditions achieved; Table 5 gives values of corresponding base shear and displacement. More in details:

Table 5.
Relevant points achieved in the analysis with corresponding values of base shear forces and displacements.
1st Distribution Forces – Shear Base Forces 2nd Distribution of Forces – Masses
A B C D A B C D
Base Force [kN] 51 258 354 362 49,5 381 392 384
Displacement [cm] 1,4 8,1 11,6 12,0 1,2 10,8 11,8 15,5
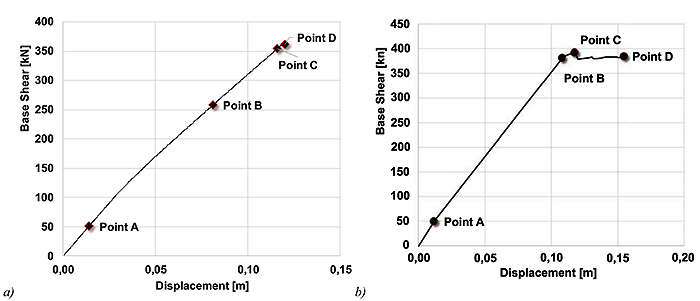
Fig. (14). Pushover analysis on DA-ARSW including compressed members in the model: a) 1st distribution of forces; b) 2nd distribution of forces.
  • Point A corresponds to a base shear of about 51 kN and a displacement of 1.4 cm. In this condition, several compressed members of the upper part of the external right shelve showed buckling phenomena.
  • Point B corresponds to a base shear equal to 258 kN and a displacement of 8.1 cm. In this condition, CP limit state was reached in several compressed braces; buckling was observed in most of the braces, while tense members did not show any specific structural problem.
  • Points C and D correspond to values of shear base of about 360 kN and displacement equal to 12 cm. Most of compressed braces reached CP limit state; strength resistance was achieved in several braces in tension.

Similar results were observed adopting the 2nd forces group (Fig. 14b). In particular:

  • Point A corresponds to a base shear force equal to 50 kN and displacement of 1.2 cm. In this condition, several compressed braces of the upper part of the external right shelve underwent buckling phenomena.
  • Points B and C correspond to values of the base shear and displacement of about 380 kN and 10-11 cm. CP was achieved in most of the braces in compression, whilst only few tense braces reached their strength capacity.
  • Point D corresponds to a displacement of about 15.5 cm. The collapse condition was reached for most of the tense braces in the bottom part of the ARSW structure.

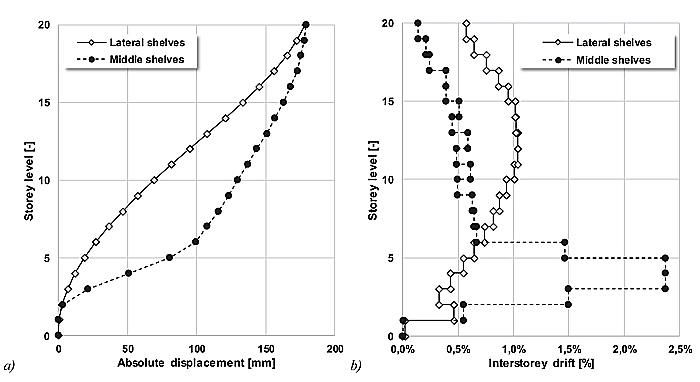
Fig. (15) shows the distribution of achieved limit states (i.e. yielding pattern) at the end of the analysis (point D) for the DA-ARSW building and the two distributions of forces. As visible, no global dissipative mechanisms were achieved: ultimate limit states were reached only in correspondence of several elements, while most of them still exhibited – at the end of the analysis – an elastic behaviour. This situation, together with the reduced absolute displacement (lower than 15 cm), was related to the concentration of deformations in correspondence of the bottom part of the DA-ARSW. This is visible from Fig. (16a), in terms of both absolute displacement and inter-storey drift. High values of inter-storey drift (up to 2.3%) were achieved in correspondence of the 4th-5th storeys of the middle shelves, while in the other areas, lower and differently distributed values were observed.

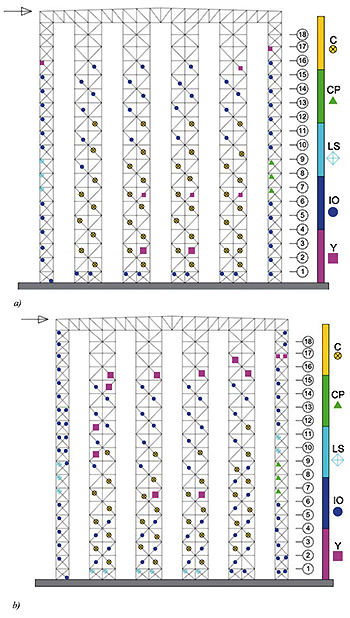
Fig. (15). Yielding patterns associated to the last step (point D) of analysis on the DA-building adopting: a) 1st and b) 2nd group distribution of forces.

Several considerations shall be made concerning this situation. One is related to the analysis method: the monitoring of the roof displacement – as commonly used in pushover analyses – is not fully representative in case of ARSW, where the shelves are connected only in correspondence of the roof, being otherwise independent along the whole height. This is evident considering the completely different behaviour of middle and lateral shelves (Fig. 16b).

Besides, the development of dissipative mechanisms takes place mainly in the bottom part of the DA-ARSW, where the overstrength variation limit is satisfied (Fig. 5): this indicates that Eurocode 8 prescriptions are not able, for this particular structural typology, to provide the full exploitation of structural ductile performance as required.

Fig. (16). a) Absolute displacements and b) interstorey drifts in correspondence of the different storeys of the ARSW for the middle and the lateral shelves (2nd group of forces).

CONCLUSION AND FUTURE WORKS

Automated Rack Supported Warehouses (ARSW) differ from traditional pallet racks (SR), being designed to resist besides self-weight and stored goods, non-structural components and equipment, environmental and seismic actions. EN 16681:2016 is then not valid for the design and the only possible reference standards are Eurocodes 3 and 8 for steel structures. But ARSW also differ from steel buildings mainly due to their geometry, e.g. high number of storeys of reduced height: the efficacy of Eurocodes’ design rules when applied to ARSW shall be then assessed.

To this aim, a case-study building was sized following an elastic and a dissipative approach. The two strategies were compared in terms of design procedure, construction feasibility, costs and structural performance.

In the dissipative Design Approach (DA) the satisfaction of the overstrength variation limit along the height imposed by Eurocode 8 was not always possible. This was mainly due to the geometry of ARSW and resulted in two non-dissipative portions located in correspondence of the bottom and of the top of the DA-ARSW (Fig. 5). The respect of slenderness limits (1.3 ≤ λ ≤ 2.0) was pursued through a wide variation of sections’ profiles along the height.

If costs related to steel material are lower in the case of EA-ARSW (9.28 tons vs 10.47 tons), connections in DA-ARSW show higher variability and higher difficulty of realization due to capacity design requirements, increasing construction costs and manpower effort.

Nonlinear static pushover analyses were adopted to assess the structural performance. EA and DA-ARSW experienced a non-uniform collapse mechanism involving only the bottom and middle parts of the structures, then disagreeing with the capacity design philosophy Figs. (7-10), Figs. (14 and 15). The application of a monotonic increasing load in correspondence to the roof storey led to the concentration of deformation/displacement at the 4th-5th levels, well represented looking at the inter-storey drift distributions obtained (Fig. 16). The global ductile behaviour imposed by Eurocode 8 is then not achieved. This situation depends, from one side, on the structural building typology and, on the other side, on the analysis method. Being the shelves connected only at the roof and independent in the bottom and intermediate portions, the representation of the behaviour by the monitoring of a single point is not strictly meaningful. To study with more accuracy the problem, nonlinear dynamic analyses with representative accelerograms shall be developed.

Results highlight then the need to develop specific design rules for ARSW, since the traditional approach proposed by Eurocodes do not allow to fully exploit the structural performance of such structures. At the same time, the necessity of improving analysis techniques to better understand and exploit the behaviour of ARSW becomes evident. The present manuscript constitutes the base for further investigations and analyses, actually ongoing in the framework of the European research project “STEELWAR: Advanced structural solutions for automated STEEL rack supported WARehouses”, funded by the Research Fund for Coal and Steel (RFCS), started in 2017 and that will end in July, 2021.

LIST OF ABBREVIATIONS

SR = Traditional Steel Pallet Racks
ARSW = Automated Rack Supported Warehouses
EA = Elastic Design Approach
DA = Dissipative Design Approach
EA-ARSW ARSW = Designed with Elastic Approach
DA-ARSW ARSW = Designed with Dissipative Approach
LS = Life Safety Limit State
IO = Immediate Occupancy Limit State
CP = Collapse Prevention Limit State
ELS = Elastic Limit State
CLS = Collapse Limit State

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

The present work has been developed in the scientific framework of the European research project “STEELWAR: Advanced structural solutions for automated STEEL rack supported WAeRhouses” funded by the Research Fund for Coal and Steel under grant agreement N. 754102.

REFERENCES

1 N. Boysen, D. Briskorn, and S. Emde, "Sequencing of picking orders in mobile rack warehouses", Eur. J. Oper. Res., vol. 259, pp. 293-3017.[CrossRef Link] 2 R. De Koster, T. Le-Duc, and K.J. Roodbergen, "Design and control of warehouse order picking: a literature review", Eur. J. Oper. Res., vol. 182, pp. 481-501.[CrossRef Link] 3 L.F. Cardona, D.F. Soto, L. Rivera, and H.J. Martínez, "Detailed design of fishbone warehouse layouts with vertical travel", Int. J. Prod. Econ., vol. 170, pp. 825-837.[CrossRef Link] 4 C. Bernuzzi, "European and United States approaches for steel storage pallet rack design. Part 1: Discussion and general comparison", Thin Wall Struct., vol. 97, pp. 308-320.[CrossRef Link] 5 C. Bernuzzi, N. Draskovic, and M. Simoncelli, "European and United States approaches for steel storage pallet rack design. Part 2: Pratical applications", Thin Wall Struct., vol. 97, pp. 321-341.[CrossRef Link] 6 A. Kaniylmaz, C.A. Castiglioni, G. Brambilla, and G.P. Chiarelli, "Experimental assessment of the seismic behavior of unbraced steel storage pallet racks", Thin Wall Struct., vol. 108, pp. 391-405.[CrossRef Link] 7 A. Kaniylmaz, G. Brambilla, G.P. Chiarelli, and C.A. Castiglioni, "Assessment of the seismic behaviour of braced steel storage racking systems by means of full scale push over tests", Thin Wall Struct., vol. 107, pp. 138-155.[CrossRef Link] 8 B. Rouwenhorst, B. Reuter, V. Stockrahm, G.J. van Hountum, R.J. Mantel, and W.H.M. Zijm, "Warehouse design and control: Framework and literature review", Eur. J. Oper. Res., vol. 122, pp. 515-533.[CrossRef Link] 9 I. Rosin, L. Calado, J. Proença, P. Carydis, H. Mouzakis, C. Castiglioni, J. C. Brescianini, A. Plumier, H. Degee, P. Negro, and F. Molina, "Seisracks: Storage racks in seismic areas", European Commission Technical report, Directorate-General for Research EUR 23744, 2009. 10 C.A. Castiglioni, A. Kanyilmaz, C. Bernuzzi, A. Drei, H. Degee, C. Braham, B. Hoffmeister, C. Heinemeyer, I. Vayas, A. Konstantinos, and S. Sesana, "Seisracks 2: Seismic behaviour of steel storage pallet racking systems ", European Commission Technical report, Directorate-General for Research EUR 27583 EN, 2014. 11 UNI EN 16681:2016 Sistemi di stoccaggio statici di acciaio - Scaffalature porta-pallet - Principi per la progettazione sismica – in italian. 12 M. Savoia, N. Buratti, and L. Vincenzi, "Damage and collapses in industrial precast buildings after the 2012 Emilia earthquake", Eng. Struct., vol. 137, pp. 162-180.[CrossRef Link] 13 F. Braga, R. Gigliotti, G. Monti, F. Morelli, C. Nuti, W. Salvatore, and I. Vanzi, "Speedup of post earthquake community recovery: The case of precast industrial buildings after the Emilia 2012 earthquake", B. Earthq Eng., vol. 12, no. 5, pp. 2405-2418.[CrossRef Link] 14 F. Braga, R. Gigliotti, G. Monti, F. Morelli, C. Nuti, W. Salvatore, and I. Vanzi, "Post-seismic assessment of existing constructions: evaluation of the shakemaps for identifying exclusion zones in Emilia", Earthq. Struct., vol. 8, no. 1, pp. 37-56.[CrossRef Link] 15 EN 1998–1:2005. Eurocode 8: design of structures for earthquake resistance. Part 1: general rules, seismic action and rules for buildings. European Committee for Standardisation, Brussels. 16 EN 1993–1:2005. Eurocode 3—design of steel structures—part 1–1: general rules and rules for buildings. 17 D.M. 17/01/2018 Italian standards for Constructions - Norme Tecniche per le Costruzioni”, Gazzetta Ufficiale della Repubblica Italiana – in italian. 18 EN1998-3:2005. Eurocode 8: Design provisions for earthquake resistance of structures— Part 3: assessment and retrofitting of buildings. European Committee for Standardisation, Brussels 19 OpenSees: Mazzoni, Silvia, et al. "The open system for earthquake engineering simulation (OpenSEES) user command-language manual", 2017. 20 M. Badalassi, A. Braconi, S. Caprili, and W. Salvatore, "Influence of steel mechanical properties on EBF seismic behaviour", B. Earthq Eng., vol. 11, pp. 2249-2285.[CrossRef Link] 21 A. Braconi, S. Caprili, H. Degee, M. Hjaij, B. Hoffmeister, S.A. Karamanos, V. Rinaldi, and W. Salvatore, "Efficiency of Eurocode 8 design rules for steel and steel-concrete composite structures", J. Constr. Steel. Res., vol. 112, pp. 108-129.[CrossRef Link] 22 M. Badalassi, A. Braconi, L.G. Cajot, S. Caprili, H. Degee, M. Gundel, M. Hjaij, B. Hoffmeister, S.A. Karamanos, W. Salvatore, and H. Somja, "Influence of variability of material mechanical properties on seismic performance of steel and steel–concrete composite structures", B. Earthq. Eng. g., vol. 15, pp. 1559-1607.